【题目】如图所示,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称。
(1)求A、B的坐标
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,P点的速度是每秒2个单位长度,Q点的速度是每秒4个单位长度,设P、Q的运动时间为t秒,当0<t<3时.
①请用含t的代数式表示三角形OPQ的面积S,
②在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足![]() ,求出点M的坐标,并求出当
,求出点M的坐标,并求出当![]() =15时,三角形OPQ的面积.
=15时,三角形OPQ的面积.
参考答案:
【答案】(1)点A的坐标为(3,4),点B的坐标为(-3,4).(2)①S=12-4t;.②点M的坐标为(-2,-2)或(10,10),当S△AQM=15时,三角形OPQ的面积是11或1.
【解析】
(1)根据A、B两点关于y轴对称可知点A、B的横坐标互为相反数,纵坐标相等,从而解答本题.
(2)①0<t<3时,点P在前,Q在后,表示出PQ的长度,即可解决问题;
②根据题意和①中求得的关系式,可以先求出点M的坐标,进而求得三角形OPQ的面积.
(1)∵A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称,
∴2a-1=3,3b+1=4.
解得a=2,b=1.
∴点A的坐标为(3,4),点B的坐标为(-3,4).
(2)①∵AP=2t,BQ=4t,AB=6,
∴当0<t<3时,PQ=6+2t-4t=6-2t;
∴当0<t<3时,S=![]() PQ×4=
PQ×4=![]() ×(6-2t)×4=12-4t;
×(6-2t)×4=12-4t;
②设点M的坐标为(x,x).
当0<t<3时,
∵S△PQM:S△OPQ=3:2,S△PQM=![]() =(3-t)×|4-x|,S△OPQ=12-4t.
=(3-t)×|4-x|,S△OPQ=12-4t.
∴![]() .
.
解得,x=-2或x=10
∴点M的坐标为(-2,-2)或(10,10)
∵S△AQM=15,即S△AQM=![]() (0<t<3),
(0<t<3),
∴t=![]() 或t=
或t=![]() ,
,
∴当t=![]() 时,S△OPQ=124×
时,S△OPQ=124×![]() =11,当t=
=11,当t=![]() 时,S△OPQ=12-4×
时,S△OPQ=12-4×![]() =1;
=1;
由上可得,点M的坐标为(-2,-2)或(10,10),当S△AQM=15时,三角形OPQ的面积是11或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线
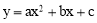 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).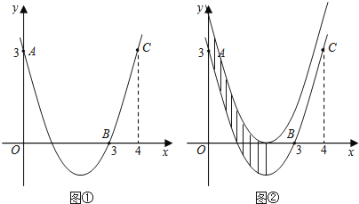
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划在规定时间内生产24000个零件.由于销售商突然急需供货,工厂实际工作效率比原计划提高了50%,并提前5天完成这批零件的生产任务.求该工厂原计划每天加工这种零件多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)
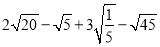
(2)
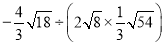
(3)
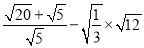
(4)
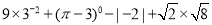
(5)
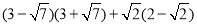
(6)
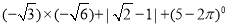
-
科目: 来源: 题型:
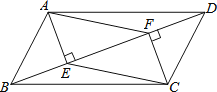
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
相关试题

