【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
参考答案:
【答案】(1)P=![]() ;(2)96kPa;(3)为了安全起见,气体的体积应不小于0.7m3.
;(2)96kPa;(3)为了安全起见,气体的体积应不小于0.7m3.
【解析】
试题分析:(1)设函数解析式为P=![]() ,把点(0.8,120)的坐标代入函数解析式求出k值,即可求出函数关系式;
,把点(0.8,120)的坐标代入函数解析式求出k值,即可求出函数关系式;
(2)把V=1m3代入求得的函数关系式即可求出P值;
(3)依题意P≤140,即![]() ≤140,解不等式即可.
≤140,解不等式即可.
试题解析:(1)设P与V的函数关系式为P=![]() ,
,
则![]() =120,
=120,
解得k=96,
所以函数关系式为P=![]() ;
;
(2)当气球内气体的体积是1m3时,
P=![]() ,
,
所以气球内气体的气压是96kPa;
(3)当P>140KPa时,气球将爆炸,
所以P≤140,即![]() ≤140kPa,
≤140kPa,
解得V≥0.7m3.
故为了安全起见,气体的体积应不小于0.7m3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知AB是⊙0的直径,AP是⊙0的切线,A是切点,BP与⊙0交于点C.
(1)如图①,若AB=2,∠P=30
 ,求AP的长.(结果保留根号)
,求AP的长.(结果保留根号)(2)如图②,若D为AP的中点,∠P=30
 ,求证:直线CD是⊙O的切线.
,求证:直线CD是⊙O的切线.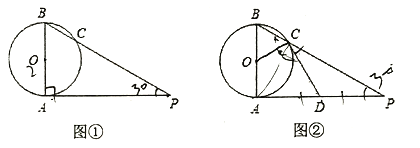
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.
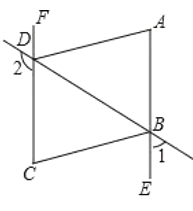
(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】盐城市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利,小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图所示的统计图,请根据图中信息,解答下列问题:

(1)这次被调査的总人数是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线
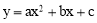 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).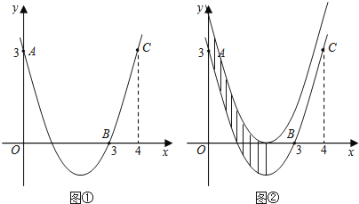
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划在规定时间内生产24000个零件.由于销售商突然急需供货,工厂实际工作效率比原计划提高了50%,并提前5天完成这批零件的生产任务.求该工厂原计划每天加工这种零件多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称。
(1)求A、B的坐标
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,P点的速度是每秒2个单位长度,Q点的速度是每秒4个单位长度,设P、Q的运动时间为t秒,当0<t<3时.
①请用含t的代数式表示三角形OPQ的面积S,
②在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足
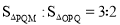 ,求出点M的坐标,并求出当
,求出点M的坐标,并求出当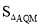 =15时,三角形OPQ的面积.
=15时,三角形OPQ的面积.
相关试题

