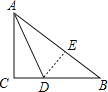
【题目】如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.
参考答案:
【答案】CD的长为3cm.
【解析】
试题分析:先根据勾股定理求出AB的长,设CD=xcm,则BD=(8﹣x)cm,再由图形翻折变换的性质可知AE=AC=6cm,DE=CD=xcm,进而可得出BE的长,在Rt△BDE中利用勾股定理即可求出x的值,进而得出CD的长.
解:∵△ABC是直角三角形,AC=6cm,BC=8cm,
∴AB=![]() =
=![]() =10cm,
=10cm,
∵△AED是△ACD翻折而成,
∴AE=AC=6cm,
设DE=CD=xcm,∠AED=90°,
∴BE=AB﹣AE=10﹣6=4cm,
在Rt△BDE中,BD2=DE2+BE2,
即(8﹣x)2=42+x2,
解得x=3.
故CD的长为3cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A.对角线互相垂直的平行四边形是正方形
B.相似三角形的周长之比等于相似的平方
C.若(1,y1)、(2,y2)是双曲线y=﹣ 上的两点,则y1<y2
上的两点,则y1<y2
D.方程x2﹣2x+3=0有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架云梯长25米,斜靠在一面墙上,梯子靠墙的一端距地面24米。(1)这个梯子底端离墙多少米?(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向也滑动了4米吗?如果不是,那滑动了几米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,E是BC的中点,过点E作EF⊥AE,交CD于点F,连接AF并延长,交BC的延长线于点G.则CG的长为( )

A.
B.1
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.
 B.
B.  C.
C. 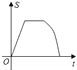 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=﹣1,x2=3.
其中正确的是( )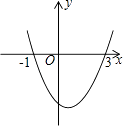
A.①②③
B.②③④
C.③④⑤
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
A. (0,4) B. (0,3) C. (﹣4,0) D. (0,﹣3)
相关试题

