【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题:
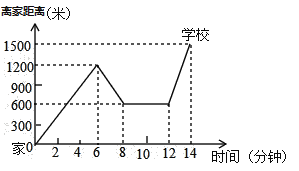
(1)小明家到学校的路程是 米,小明在书店停留了 分钟;
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(3)在整个上学的途中 (哪个时间段)小明骑车速度最快,最快的速度是 米/分;
(4)小明出发多长时间离家1200米?
参考答案:
【答案】(1)1500,4;(2)2700,14;(3)12分钟至14分钟,450;(4)小明出发6分钟或![]() 分钟离家1200米.
分钟离家1200米.
【解析】
(1)根据函数图象可以解答本题;
(2)根据函数图象可以解答本题;
(3)由函数图象可以得到哪段的速度最快,进而求得相应的速度;
(4)根据函数图象和图象中的数据,可以解答本题.
解:(1)由图象可得,
小明家到学校的路程是1500米,小明在书店停留了:![]() (分钟),
(分钟),
故答案为:1500,4;
(2)本次上学途中,小明一共行驶了:![]() (米
(米![]() ,一共用了14(分钟),
,一共用了14(分钟),
故答案为:2700,14;
(3)由图象可知,在整个上学的途中,12分钟至14分钟小明骑车速度最快,
最快的速度为:![]() 米/分钟,
米/分钟,
故答案为:12分钟至14分钟,450;
(4)设![]() 分钟时,小明离家1200米,
分钟时,小明离家1200米,
则![]() 或
或![]() ,解得
,解得![]() ,
,
即小明出发6分钟或![]() 分钟离家1200米.
分钟离家1200米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有黑、白两种颜色的球共100只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
70
124
190
325
538
670
2004
摸到白球的频率

0.70
0.62
0.633
0.65
0.6725
0.670
0.668
(1)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为 ;(精确到0.01)
(2)试估算盒子里黑球有 只;
(3)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是 .
A.从一副扑克牌中任意抽取一张,这张牌是“红色的”
B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”
C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1、y2都是x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=
 ,则函数y=min{x,
,则函数y=min{x,  }的图像应该是 中的实线部分.
}的图像应该是 中的实线部分.
(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图像,并写出该图像的三条不同性质:

① ;
② ;
③ ;
(3)函数y=min{(x-4)2, (x+2)2}的图像关于 对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km)
0
100
200
300
400
…
油箱剩余油量Q(L)
50
42
34
26
18
…
(1)该轿车油箱的容量为______L,行驶150km时,油箱剩余油量为______L;
(2)根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点D为△ABC边BC的延长线上一点.
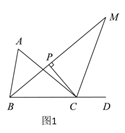
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证:
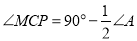 ;
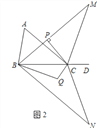
;(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正常人的体温一般在37 ℃左右,但一天中的不同时刻不尽相同,如图所示反映了一天24小时内小红的体温变化情况,下列说法错误的是 ( )

A. 清晨5时体温最低
B. 下午5时体温最高
C. 这一天小红体温T(℃)的范围是36.5≤T≤37.5
D. 从5时至24时,小红体温一直是升高的
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
相关试题

