【题目】如图1,点D为△ABC边BC的延长线上一点.
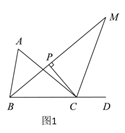
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
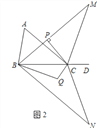
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
参考答案:
【答案】(1)60°°;
(2)证明见解析;
(3)∠BQC=90°+![]() ∠A,理由见解析.
∠A,理由见解析.
【解析】试题分析:(1)先根据∠A:∠ABC=3:4,设∠A=3k,∠ABC=4k,再由三角形外角的性质求出k的值,进而可得出结论;
(2)根据三角形外角的性质得出∠M=∠MCD-∠MBC,∠A=∠ACD-∠ABC.再由MC、MB分别平分∠ACD、∠ABC得出![]() ,
, ![]() ,
,
故![]() ,根据CP⊥BM即可得出结论;
,根据CP⊥BM即可得出结论;
(3)根据BQ平分∠CBN,CQ平分∠BCN可知![]() ,
, ![]() ,再根据三角形内角和定理可知,
,再根据三角形内角和定理可知, ![]() ,根据轴对称性质知:
,根据轴对称性质知:
∠M=∠N,由此可得出结论.
(1)解:∵![]() ,∴可设
,∴可设![]() .
.
又∵![]()
![]() °,
°,
∴![]() °,
°,
解得 ![]() °.
°.
∴![]() °.
°.
(2)证明:
![]()
(3)猜想∠BQC=90°+![]() ∠A.
∠A.
证明如下: ∵BQ平分∠CBN,CQ平分∠BCN,
∴![]() ,
,
∴![]()
![]()
![]() .
.
由(2)知: ![]() ,又由轴对称性质知:∠M=∠N,
,又由轴对称性质知:∠M=∠N,
∴![]() .
.
本题考查了三角形的内角和,三角形外角的性质,折叠的性质.(1)见比设参,然后根据外角的性质求解;(2)结合角平分线和外角的性质求解;(2)根据轴对称的性质和(2)的结论求解.
-
科目: 来源: 题型:
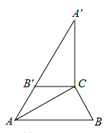
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中对称轴最多的是( )
A.圆
B.正方形
C.角
D.线段 -
科目: 来源: 题型:
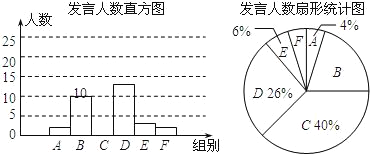
查看答案和解析>>【题目】我市某校九年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的统计图,已经知A、B两组发言人数直方图高度比为1:5.
发言次数n
A
0≤n<5
B
5≤n<10
C
10≤n<15
D
15≤n<20
E
20≤n<25
F
25≤n<30
请结E合图中相关的数据回答下列问题:
(1)A组的人数是多少?本次调查的样本容量是多少?
(2)求出C组的人数并补全直方图;
(3)该校七年级共有250人,请估计全年级每天在课堂上发言次数不少于15次的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A. 12 B. 15 C. 12或15 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动中不是平移的是( )
A. 电梯上人的升降 B. 钟表的指针的转动
C. 火车在笔直的铁轨上行驶 D. 起重机上物体的升降
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“如果a+b=0,那么a,b互为相反数”的逆命题为____________________________.
相关试题

