【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求y=-2x2+5x-3函数的“旋转函数”.
小明是这样思考的:由y=-2x2+5x-3函数可知,a1=-2,b1=5,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数y=-2x2+5x-3的“旋转函数”;
(2)若函数y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
(3)已知函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”.
(x-2)(x+3)互为“旋转函数”.
参考答案:
【答案】(1) y=2x2+5x+3 ;(2)1;(3)见解析.
【解析】
(1)根据题目中的条件直接可以写出函数表达式(2)根据a1+a2=0,b1=b2,c1+c2=0的规律列出等式进行计算即可(3)函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,求出点的坐标,再求出关于原点的对称点,进而求出经过对称点的二次函数,通过“旋转函数”的规律就可以证明两函数是互为“旋转函数”.
轴交于A、B两点,与y轴交于点C,求出点的坐标,再求出关于原点的对称点,进而求出经过对称点的二次函数,通过“旋转函数”的规律就可以证明两函数是互为“旋转函数”.
(1) y=2x2+5x+3 ;
.(2)∵y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,
x-n与y2=-x2-mx-2互为“旋转函数”,
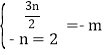 ∴解得
∴解得![]()
∴(m+n)2019=(3-2)2019 =1
(3)证明:当x=0时,y=![]() (x-2)(x+3),则C(0,-3),
(x-2)(x+3),则C(0,-3),
当y=0时,![]() (x-2)(x+3)=0,解得x1=2,x2=-3,则A(2,0),B(-3,0),
(x-2)(x+3)=0,解得x1=2,x2=-3,则A(2,0),B(-3,0),
∵点A、B、C关于原点的对称点分别是A1,B1,C1,
∴A1(-2,0),B1(3,0),C1(0,3),
可求过点A1,B1,C1的二次函数解析式为y=-![]() (x+2)(x-3)=-
(x+2)(x-3)=-![]() x2+
x2+![]() x+3…8分
x+3…8分
y=![]() (x-2)(x+3)=
(x-2)(x+3)=![]() x2+
x2+![]() x-3
x-3
∵a1+a2=![]() +(-
+(-![]() )=0,b1=b2=
)=0,b1=b2=![]() ,c1+c2=3+(-3)=0
,c1+c2=3+(-3)=0
∴经过点A1,B1,C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”
(x-2)(x+3)互为“旋转函数”
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系中作出函数
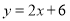 的图象,利用图象解答下列问题:
的图象,利用图象解答下列问题:
(1)求方程
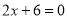 的解:
的解:(2)求不等式
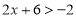 的解集;
的解集;(3)若
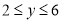 ,求
,求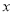 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=-x2+2x+3.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围;
③若经过点(0,k)且与x轴平行的直线l与y=-x2+2x+3的图像有公共点,求k的取值范围.
-
科目: 来源: 题型:
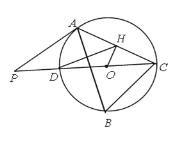
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
-
科目: 来源: 题型:
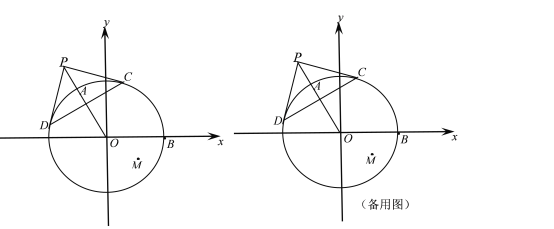
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,⊙O的圆心O在坐标原点,半径OB在x轴正半轴上,点P是⊙O外一点,连接PO,与⊙O交于点A,PC、PD是⊙O的切线,切点分别为点C、点D,AO=OB=2,∠POB=120°,点M 坐标为(1,-
 ).
).(1)求证:OP⊥CD;
(2)连结OM,求∠AOM的大小;
(3) 如果点E在x轴上,且△ABE与△AOM相似,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
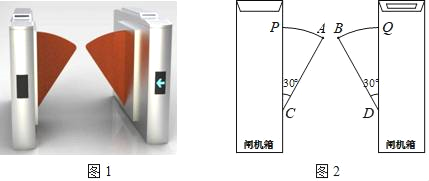
A. (54
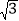 +10) cm B. (54
+10) cm B. (54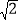 +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是( )
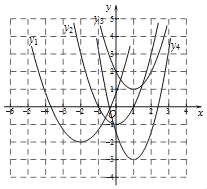
A. y1 B. y2 C. y3 D. y4
相关试题

