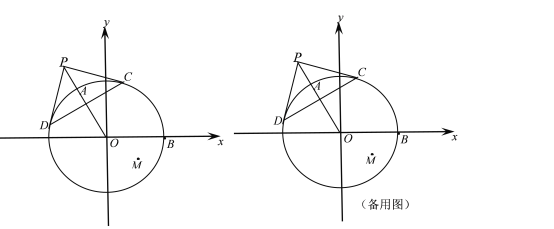
【题目】如图,在平面直角坐标系xoy中,⊙O的圆心O在坐标原点,半径OB在x轴正半轴上,点P是⊙O外一点,连接PO,与⊙O交于点A,PC、PD是⊙O的切线,切点分别为点C、点D,AO=OB=2,∠POB=120°,点M 坐标为(1,-![]() ).
).
(1)求证:OP⊥CD;
(2)连结OM,求∠AOM的大小;
(3) 如果点E在x轴上,且△ABE与△AOM相似,求点E的坐标.
参考答案:
【答案】(1)见解析;(2)150°;(3) E(4,0)或(8,0).
【解析】
(1)根据直线与圆相切的性质证明Rt△PDO ≌Rt△PCO,就可以证明OP⊥CD(2)连接OM,利用三角函数值解直角三角形即可(3)根据△ABE与△AOM相似,可以得到边,角的关系,进而得到点的坐标.
(1)连接OD、OC
∵PC、PD是⊙O的切线
∴∠PDO=∠PCO=90° ,PC=PD
∵在Rt△PDO 与Rt△PCO中
![]() ∴Rt△PDO ≌Rt△PCO(HL)
∴Rt△PDO ≌Rt△PCO(HL)
∴∠CPO=∠DPO
∵PC=PD,∠CPO=∠DPO
∴OP⊥CD
(2)连接OM,作MH⊥x轴
∵在Rt△HMO中 ∴tan∠HOM=![]() =
=![]() ∴ ∠HOM=30°
∴ ∠HOM=30°
∴ ∠AOM=∠HOM+∠POB=30°+120°=150°
(3)由OA=OB=2,∠AOB=120°,得∠ABO=30°
若点E在点B左侧时,不论∠AEB和∠EAB哪个
角等于150°,此时三角形内角和都大于180°
则点E只能在点B右侧
∵∠ABO=30°∴∠ABE=∠AOM=150°
若△ABE与△AOM相似存在两种情况
①△AOM ∽△ABE ∴![]() =
=![]()
∴ BE=2
∴E(4,0)
②△AOM ∽△EBA ∴![]() =
=![]()
∴ BE=6
∴E(8,0)
综上所述:E(4,0)或(8,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=-x2+2x+3.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围;
③若经过点(0,k)且与x轴平行的直线l与y=-x2+2x+3的图像有公共点,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求y=-2x2+5x-3函数的“旋转函数”.
小明是这样思考的:由y=-2x2+5x-3函数可知,a1=-2,b1=5,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数y=-2x2+5x-3的“旋转函数”;
(2)若函数y1=x2+
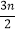 x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;(3)已知函数y=
 (x-2)(x+3)的图像与
(x-2)(x+3)的图像与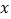 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y= (x-2)(x+3)互为“旋转函数”.
(x-2)(x+3)互为“旋转函数”. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
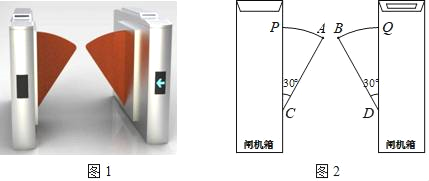
A. (54
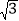 +10) cm B. (54
+10) cm B. (54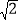 +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是( )
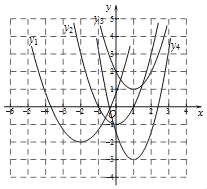
A. y1 B. y2 C. y3 D. y4
-
科目: 来源: 题型:
查看答案和解析>>【题目】近视镜镜片的焦距
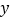 (单位:米)是镜片的度数
(单位:米)是镜片的度数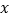 (单位:度)的函数,下表记录了一组数据:
(单位:度)的函数,下表记录了一组数据: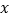 (单位:度)
(单位:度)…
100
250
400
500
…
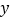 (单位:米)
(单位:米)…
1.00
0.40
0.25
0.20
…
(1)在下列函数中,符合上述表格中所给数据的是_________;
A.
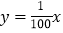 B.
B.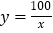 C.
C.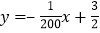 D.
D.
(2)利用(1)中的结论计算:当镜片的度数为200度时,镜片的焦距约为________米.
相关试题

