搜索
【题目】在坐标系中作出函数
的图象，利用图象解答下列问题：
（1）求方程
的解：
（2）求不等式
的解集；
（3）若
，求
的取值范围．
参考答案：
【答案】（1）
（2）
（3）
【解析】
（1）利用一次函数图像来解一元一次方程，当纵坐标为0时，横坐标的数值即为方程解.
（2）不等式
可以看作函数
的图像在函数
的图像的上方所有点的横坐标的集合.
（3）
可以看作函数
的图像和函数所截线段之间所有点的横坐标的集合.
（1）
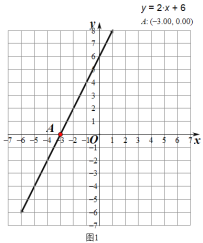
见图1，方程
的解，即为函数图像与x轴的交点，点A，即当纵坐标y为0时，横坐标x的数值，由图示得，.
（2）
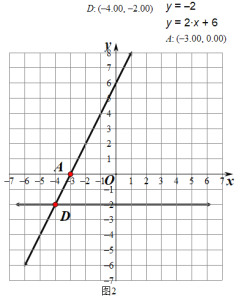
见图2，不等式的解集是函数的图像在函数 的图像的上方所有点的横坐标的集合.而两图像交点
,由图示得，.
（3）
见图3，，
的取值范围，
函数的图像和函数图像所截EF之间所有点的横坐标，由图示得.
-
科目： 来源： 题型：
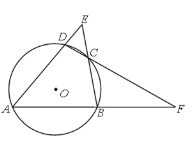
查看答案和解析>>【题目】如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F．若∠A＝50°，∠E＝45°，则∠F=____°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y＝ax2＋bx＋c上部分点的横坐标x和纵坐标y的对应值如下表，则下列说法中正确的有_______．（填序号）
x
…
－4
－3
－2
－1
0
1
…
y
…
－37
－21
－9
－1
3
3
…
①当x＞1时，y随x的增大而减小． ②抛物线的对称轴为直线x＝－
．③当x＝2时，y＝－9． ④方程ax2＋bx＋c＝0一个正数解
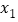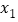满足1＜＜2． -
科目： 来源： 题型：
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．
（1）根据图示填写下表；
平均数（分）
中位数（分）
众数（分）
初中部
85
高中部
85
100
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y＝－x2＋2x＋3．
(1)求函数图像的顶点坐标，并画出这个函数的图像；
(2)根据图像，直接写出：
①当函数值y为正数时，自变量x的取值范围；
②当－2＜x＜2时，函数值y的取值范围；
③若经过点（0，k）且与x轴平行的直线l与y＝－x2＋2x＋3的图像有公共点，求k的取值范围．
-
科目： 来源： 题型：
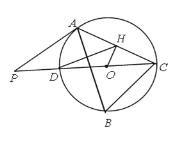
查看答案和解析>>【题目】如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝AC．
（1）求证：PA是⊙O的切线；
（2）若OH⊥AC，OH＝1，求DH的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在课外学习时遇到这样一个问题：
定义：如果二次函数y＝a1x2＋b1x＋c1（a1≠0，a1，b1，c1是常数）与y＝a2x2＋b2x＋c2
（a2≠0，a2，b2，c2是常数）满足a1＋a2＝0，b1＝b2，c1＋c2＝0，则称这两个函数互为“旋转函数”．求y＝－2x2＋5x－3函数的“旋转函数”．
小明是这样思考的：由y＝－2x2＋5x－3函数可知，a1＝－2，b1＝5，c1＝－3，根据a1＋a2＝0，b1＝b2，c1＋c2＝0，求出a2，b2，c2就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面的问题：
（1）写出函数y＝－2x2＋5x－3的“旋转函数”；
（2）若函数y1＝x2＋
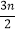x－n与y2＝－x2－mx－2互为“旋转函数”，求（m＋n）2019的值；（3）已知函数y＝
(x－2)(x＋3)的图像与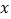
轴交于A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是A1、B1、C1，试证明经过点A1、B1、C1的二次函数与函数y＝ (x－2)(x＋3)互为“旋转函数”．
相关试题
