【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,M是AB上的动点
,M是AB上的动点![]() 不与A、B重合
不与A、B重合![]() ,过点M作
,过点M作![]() 交AC于点N,以MN为直径作
交AC于点N,以MN为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() 设
设![]() .
.
![]() 的面积
的面积![]() ______,
______,![]() ______;
______;![]() 用含x的代数式表示
用含x的代数式表示![]()
![]() 在动点M的运动过程中,设
在动点M的运动过程中,设![]() 与四边形MNCB重合部分的面积为
与四边形MNCB重合部分的面积为![]() 试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?

参考答案:
【答案】(1)![]() ;
;![]() ;(2)y关于x的函数表达式为
;(2)y关于x的函数表达式为 ,当
,当![]() 时,y的值最大,最大值为
时,y的值最大,最大值为![]() .
.
【解析】
![]() 在
在![]() 中,利用勾股定理可求出BC的值,由
中,利用勾股定理可求出BC的值,由![]() ,利用平行线分线段成比例可求出AN、MN的值,再利用三角形的面积公式结合矩形的性质即可求出
,利用平行线分线段成比例可求出AN、MN的值,再利用三角形的面积公式结合矩形的性质即可求出![]() 的面积S的值;
的面积S的值;
![]() 分
分![]() 及
及![]() 两种情况考虑:
两种情况考虑:![]() 当
当![]() 时,利用
时,利用![]() 的结论可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值;
的结论可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值;![]() 当
当![]() 时,由
时,由![]() 可得出BM、PF的值,利用三角形的面积公式结合
可得出BM、PF的值,利用三角形的面积公式结合![]() 可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值
可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值![]() 综上,此题得解.
综上,此题得解.
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() 四边形AMPN为矩形,
四边形AMPN为矩形,
![]() .
.
故答案为:![]() ;
;![]()
![]() 当点M为线段AB中点时,点P落在线段BC上,
当点M为线段AB中点时,点P落在线段BC上,
![]() 分
分![]() 及
及![]() 两种情况考虑.
两种情况考虑.
![]() 当
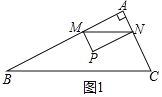
当![]() 时,如图1所示.
时,如图1所示.
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,y取最大值,最大值为1;
时,y取最大值,最大值为1;
![]() 当
当![]() 时,如图2所示.
时,如图2所示.

![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 当x取
当x取![]() 时,y取最大值,最大值为
时,y取最大值,最大值为![]() .
.
综上所述:y关于x的函数表达式为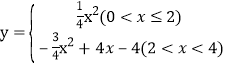 ,
,
当![]() 时,y的值最大,最大值为
时,y的值最大,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘外卖送餐员,送餐员的月工资由底薪1000元加上外卖送单补贴
 送一次外卖称为一单
送一次外卖称为一单 构成,外卖送单补贴的具体方案如下:
构成,外卖送单补贴的具体方案如下:外卖送单数量
补贴
 元
元 单
单
每月不超过500单
6
超过500单但不超过m单的部分

8
超过m单的部分
10
 若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元? 设5月份某“外卖小哥”送餐x单
设5月份某“外卖小哥”送餐x单 ,所得工资为y元,求y与x的函数关系式.
,所得工资为y元,求y与x的函数关系式. 若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.
若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市投入31500元购进A、B两种饮料共800箱,饮料的成本与销售价如下表:(单位:元/箱)
类别
成本价
销售价
A
42
64
B
36
52
(1)该超市购进A、B两种饮料各多少箱?
(2)全部售完800箱饮料共盈利多少元?
(3)若超市计划盈利16200元,且A类饮料售价不变,则B类饮料销售价至少应定为每箱多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠1=∠2,EG平分∠AEC.

(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.求证:AB∥CD;
(2)如图②,∠MAE=140°,∠FEG=30°,当∠NCE= °时,AB∥CD;
(3)如图②,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD;
(4)如图③,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的顶点A、D分别落在x轴、y轴,OD=2OA=6,AD:AB=3:1.则点B的坐标是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AD∥BC,M为CD中点,AM平分∠DAB,AD+BC=AB.求证:BM平分∠ABC.

小淇证明过程如下:
延长BC至点F,使得CF=AD,连接MF.
∵ AD∥BC, ∴ ∠D=∠MCF.
∵ M为CD中点,∴ DM=CM.
在△ADM和△FCM中,

∴ △ADM≌△FCM(SAS). ∴ AM=FM.
∵ BF=BC+CF=BC+AD=AB,∴ △ABF是等腰三角形.
∴ BM平分∠ABC(等腰三角形底边上的中线与顶角的角平分重合).
(1)请你简要叙述小淇证明方法的错误之处;
(2)若AB=5,AM=3,求四边形ABCD面积.
相关试题

