【题目】已知:如图,在四边形ABCD中,AD∥BC,M为CD中点,AM平分∠DAB,AD+BC=AB.求证:BM平分∠ABC.

小淇证明过程如下:
延长BC至点F,使得CF=AD,连接MF.
∵ AD∥BC, ∴ ∠D=∠MCF.
∵ M为CD中点,∴ DM=CM.
在△ADM和△FCM中,

∴ △ADM≌△FCM(SAS). ∴ AM=FM.
∵ BF=BC+CF=BC+AD=AB,∴ △ABF是等腰三角形.
∴ BM平分∠ABC(等腰三角形底边上的中线与顶角的角平分重合).
(1)请你简要叙述小淇证明方法的错误之处;
(2)若AB=5,AM=3,求四边形ABCD面积.
参考答案:
【答案】(1)见解析;(2)12.
【解析】
(1)根据题中的证明过程可知错误之处在于没有证明A,M,F三点共线;
(2)延长AM、BC交于点F,先证明△ADM≌△FCM,再证明△ABF是等腰三角形,利用三线合一的性质可得BM⊥AF,然后求出BM和AF可得△ABF的面积,再证明四边形ABCD面积等于△ABF的面积即可.
解:(1)小淇证明方法的错误之处在于没有证明A,M,F三点共线,故无法运用等腰三角形三线合一的性质证明BM平分∠ABC;
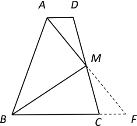
(2)如图,延长AM、BC交于点F.
∵AD∥BC,
∴∠D=∠MCF,
在△ADM和△FCM中,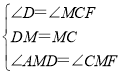 ,
,
∴△ADM≌△FCM(ASA),
∴AD=CF,AM=MF,S△ADM=S△FCM,
∵AD+BC=AB,
∴BC+CF=BC+AD=BF=AB,
∵AB=BF,AM=MF,
∴BM⊥AF,
∵AB=5,AM=3,
∴BM=4,AF=6,
∴S△ABF=![]() ,
,
∴四边形ABCD面积=S四边形ABCM + S△ADM= S四边形ABCM+ S△FCM= S△ABF=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,M是AB上的动点
,M是AB上的动点 不与A、B重合
不与A、B重合 ,过点M作
,过点M作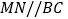 交AC于点N,以MN为直径作
交AC于点N,以MN为直径作 ,并在
,并在 内作内接矩形
内作内接矩形 设
设 .
. 的面积
的面积 ______,
______, ______;
______; 用含x的代数式表示
用含x的代数式表示
 在动点M的运动过程中,设
在动点M的运动过程中,设 与四边形MNCB重合部分的面积为
与四边形MNCB重合部分的面积为 试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的顶点A、D分别落在x轴、y轴,OD=2OA=6,AD:AB=3:1.则点B的坐标是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,直线l∥AB,P是直线l上一动点.对于下列各值:①线段AB的长②△PAB的周长③△PAB的面积④∠APB的度数其中不会随点P的移动而变化的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请画出平移后的△A'B'C',并求△A'B'C'的面积= ;
(2)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP;
(3)请在图中画出过点C且平行于AB的直线CM.

相关试题

