【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


参考答案:
【答案】(1)55m;(2)54.5m; (3)答案不唯一,如54.75 m或54.8 m
【解析】试题分析:(1)由题意,可得△ABC∽△DEC,根据相似三角形对应边的比等于相似比进行求解即可得;
(2)在Rt△ABC中,根据∠ACB的正切进行计算即可得;
(3)答案只要在上面两个小题的结果范围内即可.
试题解析:(1)由题意,可得△ABC∽△DEC,∴![]() ,
,
即![]() ,解得:AB=55,
,解得:AB=55,
答:该塔的高度为55m;
(2)在Rt△ABC中,tan∠ACB=![]() ,
,
∴AB=(48+2)×tan47.5°≈50×1.09=54.4(m),
答:该塔的高度为54.5m.
(3)答案不唯一,如54.75 m或54.8 m(数值在54.5~55之间均可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
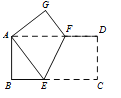
A. AF=AE B. △ABE≌△AGF C. EF=
 D. AF=EF
D. AF=EF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在长方形
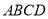 中,对角线
中,对角线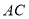 与
与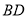 交于点O,动点P从点A出发,沿
交于点O,动点P从点A出发,沿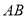 匀速运动,到达点B时停止,设点P所走的路程为x.线段
匀速运动,到达点B时停止,设点P所走的路程为x.线段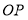 的长为y,若y与x之间的函数图象如图2所示,图象与y轴的交点为E.则E的纵坐标为_______________,则长方形
的长为y,若y与x之间的函数图象如图2所示,图象与y轴的交点为E.则E的纵坐标为_______________,则长方形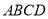 的周长为____________.
的周长为____________.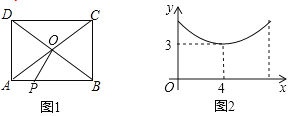
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
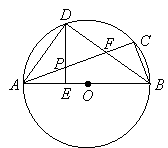
【1】求证:∠DAC =∠DBA;
【2】求证:
 是线段AF的中点
是线段AF的中点【3】若⊙O 的半径为5,AF =
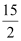 ,求tan∠ABF的值.
,求tan∠ABF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三点,点A和点B间距20个单位长度且点A、B表示的有理数互为相反数,AC=36,数轴上有一动点P从点A出发,以每秒1个单位长度的速度沿数轴向终点C移动,设移动时间为t秒.
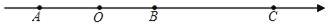
(1)点A表示的有理数是 ,点B表示的有理数是 ,点C表示的有理数是 .
(2)当点P运动到点B时,点Q从点O出发,以每秒6个单位长度的速度沿数轴在点O和点C之间往复运动.
①求t为何值时,点Q第一次与点P重合?
②当点P运动到点C时,点Q的运动停止,求此时点Q一共运动了多少个单位长度,并求出此时点Q在数轴上所表示的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使2AD=AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.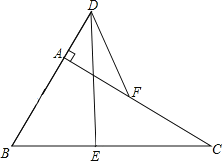
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动
问题情境:
如图1,在ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将ADE绕点A顺时针旋转α角(0°<α<90°)得到AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
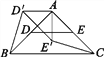 图1
图1 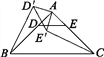 图2
图2 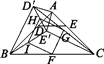 图3
图3 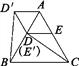 图4
图4探究发现:
(1)图1中,CE′与BD′的数量关系是________;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E”,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在(2)的条件下,连接BE′,CD′,分别取BC,CD′,E′D′,BE′的中点F,G,H,I,顺次连接F,G,H,I得到四边形FGHI.请判断四边形FGHI的形状,并说明理由;
(4)如图4,在ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将ADE绕点A顺时针旋转60°得到AD′E′,连接CE′,BD′.请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
相关试题

