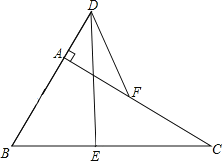
【题目】如图,在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使2AD=AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.
参考答案:
【答案】(1)说明见解析;(2)2.
【解析】试题分析:(1)连接EF、AE,证四边形AEFD是平行四边形即可.
(2)注意应用直角三角形斜边上的中线等于斜边的一半和平行四边形的性质:平行四边形的对边相等,求得AE长即可.
试题解析:(1)连接EF,AE.
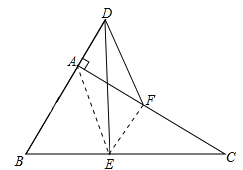
∵点E,F分别为BC,AC的中点,
∴EF∥AB,EF=![]() AB.
AB.
又∵AD=![]() AB,
AB,
∴EF=AD.
又∵EF∥AD,
∴四边形AEFD是平行四边形.
∴AF与DE互相平分.
(2)在Rt△ABC中,
∵E为BC的中点,BC=4,
∴AE=![]() BC=2.
BC=2.
又∵四边形AEFD是平行四边形,
∴DF=AE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△A′B′C′,∠A=80°,∠B=40°,那么∠C′的度数为( )
A. 80°
B. 40°
C. 60°
D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体中,正视图、左视图、俯视图完全相同的是( )
A.圆柱
B.圆锥
C.棱锥
D.球 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=- 2x2 - 4x - 5经过平移后得到抛物线y=- 2x2,平移方法是( )
A. 向左平移1个单位,再向下平移3个单位
B. 向左平移1个单位,再向上平移3个单位
C. 向右平移1个单位,再向下平移3个单位
D. 向右平移1个单位,再向上平移3个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
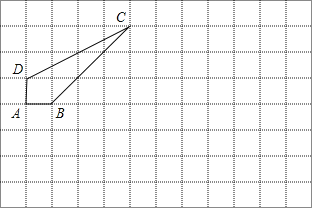
(1)以B为坐标原点,AB所在直线为x轴,建立直角坐标系;
(2)写出四边形各顶点的坐标;
(3)计算四边形的面积;
(4)画出将四边形向右平移5个单位,向下平移2个单位得到的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
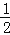 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).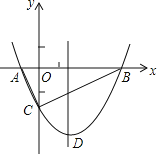
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设图中每个小正方形的边长为1,
(1)请画出△ABC关于y轴对称图形△A’B’C’,其中ABC的对称点分别为A’B’C’)
(2)直接写出A’B’C’的坐标:A’B’C’
相关试题

