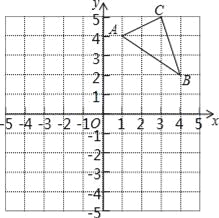
【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．

（1）请画出△A1B1C1，使△A1B1C1与△ABC关于x轴对称；

（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出点B旋转到点B2所经过的路径长．

参考答案：

【答案】（1）画图参见解析；（2）画图参见解析，路径长为π．

【解析】试题分析：（1）根据网格结构找出点A、B、C关于x轴的对称点A1、B1、C1的位置，然后顺次连接即可；

（2）根据网格结构找出点A、B、C绕点O逆时针旋转90°的对应点A2、B2、C2的位置，然后顺次连接，再利用弧长公式进行计算即可.

试题解析：（1）如图所示，△A1B1C1即为所求；

（2）如图所示，△A2B2C2即为所求，

∵OB=，∠BOB2=90°，

∴点B旋转到点B2所经过的路径长为．

关闭