【题目】如图(1)所示,∠AOB、∠COD都是直角.
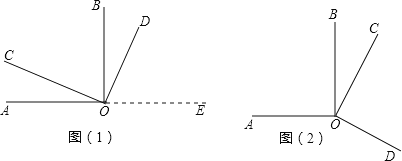
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
参考答案:
【答案】(1)∠AOD与∠COB互补;(2)成立,证明见解析
【解析】
试题分析:(1)根据直角的定义可得∠AOB=∠COD=90°,然后用∠AOD和∠COB表示出∠BOD,列出方程整理即可得解;
(2)根据周角等于360°列式整理即可得解.
解:(1)∠AOD与∠COB互补.
理由如下:∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°,
∠BOD=∠COD﹣∠COB=90°﹣∠COB,
∴∠AOD﹣90°=90°﹣∠COB,
∴∠AOD+∠COB=180°,
∴∠AOD与∠COB互补;
(2)成立.
理由如下:∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∵∠AOB+∠BOC+∠COD+∠AOD=360°,
∴∠AOD+∠COB=180°,
∴∠AOD与∠COB互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,数值相等的是( )
A.﹣23和(﹣2)3
B.32和23
C.﹣32和(﹣3)2
D.﹣(3×2)2和﹣3×22 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),
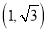 ,将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2.将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得△OBnCn.
,将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2.将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得△OBnCn.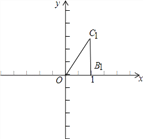
(1)m的值是___;
(2)△OB2016C2016中,点C2016的坐标:______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到 “分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数
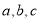 满足
满足 ,求
,求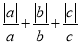 的值.
的值.【解决问题】
解:由题意,得
 三个有理数都为正数或其中一个为正数,另两个为负数.
三个有理数都为正数或其中一个为正数,另两个为负数.①
 都是正数,即
都是正数,即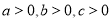 时,则
时,则 ;
;②当
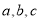 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设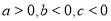 ,则
,则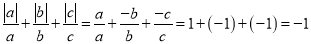 .
.综上所述,
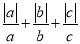 值为3或-1.
值为3或-1.【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数
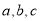 满足
满足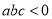 ,求
,求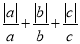 的值;
的值;(2)若
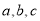 为三个不为0的有理数,且
为三个不为0的有理数,且 ,求
,求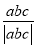 的值
的值 -
科目: 来源: 题型:
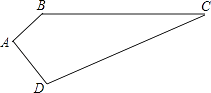
查看答案和解析>>【题目】如图,四边形ABCD,已知∠A=90°,AB=3,BC=12,CD=13,DA=4.求四边形的面积.
相关试题

