【题目】如图,四边形ABCD,已知∠A=90°,AB=3,BC=12,CD=13,DA=4.求四边形的面积. 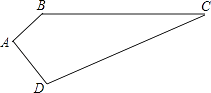
参考答案:
【答案】解:连接BD, ∵AB=3,BC=12,CD=13,DA=4,∠A=90°,
∵BD= ![]() =5,
=5,
∴BD2+BC2=CD2 ,
∴△BCD均为直角三角形,
∴S四边形ABCD的面积=S△ABD+S△BCD= ![]() ABAD+
ABAD+ ![]() BCBD=
BCBD= ![]() ×3×4+
×3×4+ ![]() ×12×5=36.
×12×5=36.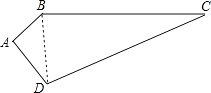
【解析】连接BD可得△ABD与△BCD均为直角三角形,进而可求解四边形的面积.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,∠AOB、∠COD都是直角.
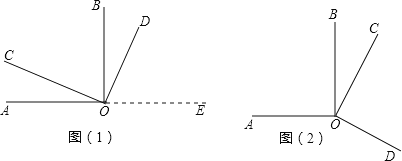
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),
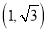 ,将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2.将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得△OBnCn.
,将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2.将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得△OBnCn.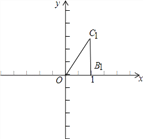
(1)m的值是___;
(2)△OB2016C2016中,点C2016的坐标:______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到 “分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数
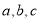 满足
满足 ,求
,求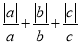 的值.
的值.【解决问题】
解:由题意,得
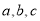 三个有理数都为正数或其中一个为正数,另两个为负数.
三个有理数都为正数或其中一个为正数,另两个为负数.①
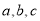 都是正数,即
都是正数,即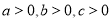 时,则
时,则 ;
;②当
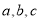 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设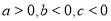 ,则
,则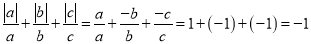 .
.综上所述,
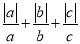 值为3或-1.
值为3或-1.【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数
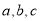 满足
满足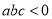 ,求
,求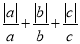 的值;
的值;(2)若
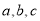 为三个不为0的有理数,且
为三个不为0的有理数,且 ,求
,求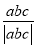 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式.
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的解析式.
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.

①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承担了加工2100个机器零件的任务,甲车间单独加工了900个零件后,由于任务紧急,要求乙车间与甲车间同时加工,结果比原计划提前12天完成任务.已知乙车间的工作效率是甲车间的1.5倍,求甲、乙两车间每天加工零件各多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定※是一种新的运算符号,且a※b=ab+a+b,例如:2※3=2×3+2+3=11,那么(3※4)※1=( )
A.19
B.29
C.39
D.49
相关试题

