【题目】如图,直线l上有A、B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
![]()
(1)OA= cm,OB= cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为ts.当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP-OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
参考答案:
【答案】(1)OA=8cm,OB=4cm;(2)![]() ;(3)① 当P在点O左侧时,
;(3)① 当P在点O左侧时,![]() ;当P在点O右侧时,t=8;② 24cm
;当P在点O右侧时,t=8;② 24cm
【解析】
试题分析:(1)由于AB=12cm,点O是线段AB上的一点,OA=2OB,则OA+OB=3OB=AB=12cm,依此即可求解;(2)根据图形可知,点C是线段AO上的一点,可设CO的长是xcm,根据AC=CO+CB,列出方程求解即可;(3)①分0≤t<4;4≤t<6;t≥6三种情况讨论求解即可;②求出点P经过点O到点P,Q停止时的时间,再根据路程=速度×时间即可求解.
试题解析:(1)∵AB=12cm,OA=2OB,
∴OA+OB=3OB=AB=12cm,解得OB=4cm,
OA=2OB=8cm.
设CO的长是xcm,依题意有,8-x=x+4+x,
解得x=![]() .
.
故CO的长是![]() cm;
cm;
①当0≤t<4时,依题意有,2(8-2t)-(4+t)=4,
解得t=1.6;
当4≤t<6时,依题意有,2(2t-8)-(4+t)=4,
解得t=8(不合题意舍去);
当t≥6时,依题意有,2(2t-8)-(4+t)=4,
解得t=8.
故当t为1.6s或8s时,2OP-OQ=4;
②[4+(8÷2)×1]÷(2-1)
=[4+4]÷1
=8(s),
3×8=24(cm).
答:点M行驶的总路程是24cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3a﹣(2a﹣b)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2a+1,4)与P'(1,3b﹣1)关于原点对称,则2a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论: ①△AED≌△AEF
②△AED为等腰三角形
③BE+DC>DE
④BE2+DC2=DE2 ,
其中正确的有( )个.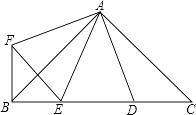
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣1)2+2图象的顶点坐标是( )
A.(2,﹣1)B.(2,1)C.(﹣1,2)D.(1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: ①甲船的速度是25km/h;
②从A港到C港全程为120km;
③甲船比乙船早1.5小时到达终点;
④图中P点为两者相遇的交点,P点的坐标为(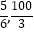 );
);
⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是 <x<2.
<x<2.
其中正确的结论有 .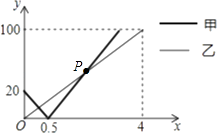
相关试题

