【题目】某商店经营一种成本为每千克40美元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为多少元时,获得的利润最大?最大利润是多少?
参考答案:
【答案】解:设销售单价定为每千克x元,获得利润为w元,则: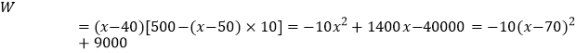
∴当x=70时,利润最大为9000元.
答:销售单价定为70元时获得的利润最大,最大利润是9000元
【解析】解决最值问题的基本策略是函数思想,构建以销售单价x为自变量,利润为因变量的函数,再利用配方法求出最值.
【考点精析】通过灵活运用二次函数的最值,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面所给的平面直角坐标系中,解答下列问题
(1)描出点A(﹣2,0),B(2,﹣1),C(3,3),并用线段依次连接起来.
(2)将三角形ABC向左平移2个单位长度,再向下平移3个单位长度,得到三角形A′B′C′.
(3)写出三角形A′B′C′各个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.

(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,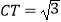 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数
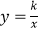 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).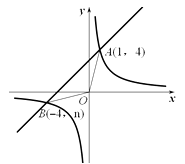
(1)求△OAB的面积;
(2)根据图象,直接写出不等式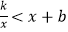 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与  轴交
轴交  、
、  两点,直线
两点,直线  与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.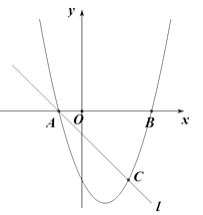
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次篮球联赛初赛阶段,每队有
 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得 分, 负一场得
分, 负一场得 分,积分超过
分,积分超过 分才能获得参赛资格.
分才能获得参赛资格.(1)已知甲队在初赛阶段的积分为
 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】青少年“心理健康”问题已经引起了社会的关注,某中学对全校850名学生进行了一次“心理健康”知识测试,并从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本,列出下面的频数分布表(单位:分)
成绩
50.5≤x<60.5
60.5≤x<70.5
70.5≤x<80.5
80.5≤x<90.5
90.5≤x<100.5
频数
2
8
10
16
14
(1)组距是 ,组数是 .
(2)成绩在60.5≤x<80.5范围的频数是 .
(3)画出频数分布直方图.
(4)若成绩在80分以上(不含80分)为优秀,试估计该校成绩优秀的有多少人?
相关试题

