【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2, ![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】
(1)证明:连接OT,
∵OA=OT,
∴∠OAT=∠OTA,
又∵AT平分∠BAD,
∴∠DAT=∠OAT,
∴∠DAT=∠OTA,
∴OT∥AC,
又∵CT⊥AC,
∴CT⊥OT,
∴CT为⊙O的切线
(2)解:过O作OE⊥AD于E,则E为AD中点,
又∵CT⊥AC,
∴OE∥CT,
∴四边形OTCE为矩形
∵CT= ![]() ,
,
∴OE= ![]() ,
,
又∵OA=2,
∴在Rt△OAE中, ![]()
![]() =1,
=1,
∴AD=2AE=2
【解析】(1)要证相切,可证CT⊥OT,由CT⊥AC,需证OT∥AC,即证出∠DAT=∠OTA,进而得出CT为⊙O的切线;(2)求弦长需作垂线,构造出弦心距,利用勾股定理求出弦的一半,进而求出整个弦长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程.
如图,已知,∠1+∠2=180°,∠A=∠D.求证AB∥CD.
证明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 为坐标原点,已知点
为坐标原点,已知点 ,将
,将 绕坐标原点
绕坐标原点 旋转90°到
旋转90°到 ,则点
,则点 的坐标是__________.
的坐标是__________. -
科目: 来源: 题型:
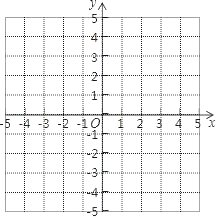
查看答案和解析>>【题目】在下面所给的平面直角坐标系中,解答下列问题
(1)描出点A(﹣2,0),B(2,﹣1),C(3,3),并用线段依次连接起来.
(2)将三角形ABC向左平移2个单位长度,再向下平移3个单位长度,得到三角形A′B′C′.
(3)写出三角形A′B′C′各个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数
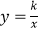 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).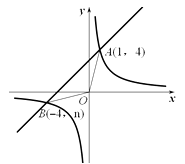
(1)求△OAB的面积;
(2)根据图象,直接写出不等式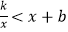 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经营一种成本为每千克40美元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为多少元时,获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与  轴交
轴交  、
、  两点,直线
两点,直线  与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.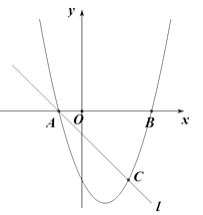
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
相关试题

