【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣2
x﹣2![]() 与x轴交于A,B两点(点A在点B的左侧),交y轴于点C.
与x轴交于A,B两点(点A在点B的左侧),交y轴于点C.
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;
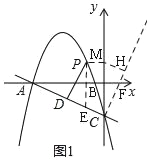
(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.
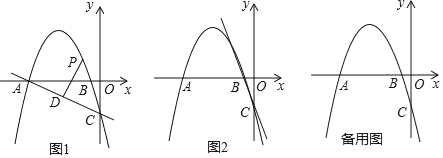
参考答案:
【答案】(1)y=﹣![]() x﹣2
x﹣2![]() ;(2)M(0,
;(2)M(0,![]() ),(3)(
),(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】分析:(1)、根据题意分别求出点A和点C的坐标,然后利用待定系数法求出函数解析式;(2)、过点P作PE∥y轴交直线AC于点E,设出点P的坐标,从而得出PE的长度,根据△PDE和△AOC相似得出PD的长度,然后证明出△CHM和△COF相似,△PKM和△COF相似,从而求出点M的坐标;(3)、根据菱形的性质分别分五种情况进行讨论,得出点P的坐标.
详解:(1)当y=0时,﹣![]() x2﹣
x2﹣![]() x﹣2
x﹣2![]() =0,解这个方程,得:x1=﹣6,x2=﹣1,
=0,解这个方程,得:x1=﹣6,x2=﹣1,
∴点A(﹣6,0),B(﹣1,0), 当x=0时,y=﹣2![]() , ∴C(0,﹣2
, ∴C(0,﹣2![]() ),
),
设直线AC的解析式为:y=ax+b(a≠0),
将点A(﹣6,0),C(0,﹣2![]() )代入得:
)代入得:![]() , ∴
, ∴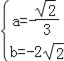 ,
,
∴直线AC的解析式为:y=﹣![]() x﹣2
x﹣2![]() ;
;
(2)如图1,过点P作PE∥y轴交直线AC于点E,
设P(a,﹣![]()
![]() ﹣2
﹣2![]() ),
),
∴PE=(﹣![]() )﹣(﹣
)﹣(﹣![]() ﹣2
﹣2![]() )=﹣
)=﹣![]() ﹣2
﹣2![]() a,
a,
∵AO=6,OC=2![]() , ∴AC=
, ∴AC=![]() =
=![]() =2
=2![]() ,
,
∵∠PDE=∠AOC=90°,∠PED=∠ACO, ∴△PDE∽△AOC, ∴![]() =
=![]() ,
,
∴PD=![]() PE=
PE=![]() =﹣
=﹣![]() ﹣
﹣![]() , 对称轴是:a=﹣3,
, 对称轴是:a=﹣3,
∵﹣![]() ,
,
∴当a=﹣3时,PD的长度最大,此时点P的坐标为(﹣3,2![]() ),
),
如图1所示,在x轴上取点F(1,0),连接CF并延长,
∴CF=![]() =
=![]() =3, ∴sin∠OCF=
=3, ∴sin∠OCF=![]() =
=![]() ,
,
点M是y轴上一点,过点M作MH⊥CF于点H,
由△CHM∽△COF,可知:![]() =
=![]() , ∵t=
, ∵t=![]() =PM+MH,
=PM+MH,
如图2,当P、M、H在同一直线上时,t的值最小,此时,过P作PK⊥y轴于K,
由△PKM∽△COF,可知:![]() =2
=2![]() , ∴KM=
, ∴KM=![]() , ∴M(0,
, ∴M(0,![]() ),
),
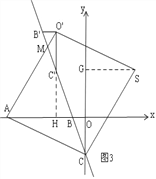
(3)如图3,当四边形ACSO'是菱形时,过S作SG⊥y轴于G,延长O'C'交x轴于H,
∵四边形ACSO'是菱形, ∴AO'=AC=SC,AO'∥SC, ∴∠AMC=∠BCS,
∴∠AO'H+∠MC'O'=∠BCO+∠OCS, ∵∠MC'O'=∠BCO, ∴∠AO'H=∠OCS,
∵∠AHO'=∠CGS, ∴△O'AH≌△CSG, ∴AH=SG,O'H=CG,
Rt△OCB中,sin∠OCB=![]() =
=![]() , ∴sin∠BC'H=
, ∴sin∠BC'H=![]() =
=![]() ,
,
设BH=x,则BC'=3x, ∴C'H=2![]() x, ∴AH=SG=5﹣x, ∵O'C'=OC=2
x, ∴AH=SG=5﹣x, ∵O'C'=OC=2![]() ,
,
∴C'H=OG=2![]() x, 由勾股定理得:AC2=O'A2, ∴AO2+OC2=O'H2+AH2,
x, 由勾股定理得:AC2=O'A2, ∴AO2+OC2=O'H2+AH2,
∴![]() =(5﹣x)2+(2
=(5﹣x)2+(2![]() +2
+2![]() x)2, 解得:x=
x)2, 解得:x=![]() ,
,
当x=![]() 时,SG=5﹣x=
时,SG=5﹣x=![]() ,OG=2
,OG=2![]() x=
x=![]() ,
,
当x=![]() <0时,不符合题意,舍去,SG=5﹣x=
<0时,不符合题意,舍去,SG=5﹣x=![]() ,OG=2
,OG=2![]() x=
x=![]() ,
,
此时S的坐标为:![]() 或
或![]() ;
;
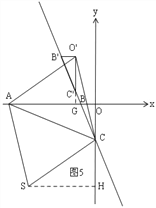
②如图4,过S作SH⊥AO于H,延长O'B'到y轴交于G, ∵SE∥CF,EC∥SF,
∴四边形SECF是平行四边形, ∴∠ESF=∠ECF, ∵四边形ASO'C是菱形,
∴∠ASO'=∠ACO', ∴∠ASH=∠O'CG, 同理得:△ASH≌△O'CG, ∴AH=O'G,SH=CG,
sin∠GCB'=![]() =
=![]() , 设GB'=x,则CB'=3x,CG=2
, 设GB'=x,则CB'=3x,CG=2![]() x, ∴O'G=1+x,
x, ∴O'G=1+x,
由勾股定理得:AC2=O'C2, ∴62+(2![]() )2=(2
)2=(2![]() x)2+(x+1)2,解得:x=
x)2+(x+1)2,解得:x=![]() ,
,
当x=![]() 时,SH=CG=2
时,SH=CG=2![]() x=
x=![]() ,OH=6﹣AH=6﹣O'G=5﹣x=
,OH=6﹣AH=6﹣O'G=5﹣x=![]() ,
,
当x=![]() <0时,不符合题意,舍去,
<0时,不符合题意,舍去,
此时,点S的坐标为:(![]() ,
,![]() );
);
③如图5,AC为对角线时,同理可得S(![]() ,
,![]() )
)
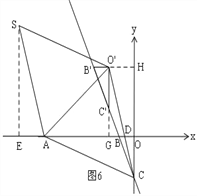
④如图6,过S作SE⊥x轴于E,延长B'O'交y轴于H,延长O'C'交x轴于G,
设GB'=x,则CB'=3x,CG=2![]() x, ∴O'G=O'H=1+x, ∵∠HO'D=∠O'DA=∠EAS,
x, ∴O'G=O'H=1+x, ∵∠HO'D=∠O'DA=∠EAS,
易得△SEA≌△CHO', 同理可得S(![]() ,
,![]() );
);
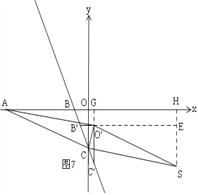
⑤如图7,过S作SH⊥x轴于H,过O'作O'E⊥SH于E,延长C'O'交x轴于G,
设OG=x,则BG=1+x, ∵O'B'∥BG, ∴![]() , ∴
, ∴![]() ,
,
∴C'G=2![]() (1+x), ∴O'G=C'G﹣C'O'=2
(1+x), ∴O'G=C'G﹣C'O'=2![]() x, ∴AG=1+x,
x, ∴AG=1+x,
同理得:62+(2![]() )2=(1+x)2+(2
)2=(1+x)2+(2![]() x)2,
x)2,
解得:x1=![]() ,x2=
,x2=![]() (舍), 可得S
(舍), 可得S![]() ;
;
综上所述,S的坐标为:![]() 或
或![]() 或(
或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张长方形纸片,
 长为
长为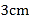 ,
,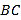 长为
长为 .
. 
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕
 边所在直线旋转一周,则形成的几何体的体积是____
边所在直线旋转一周,则形成的几何体的体积是____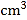 (结果保留
(结果保留 );
);(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留
 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】把两个全等的等腰直角三角形如图放置在一起
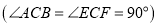 ,点
,点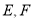 关于
关于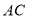 对称
对称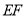 交
交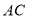 ,
,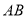 于点
于点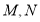 ,则
,则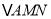 与
与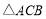 的面积比为( )
的面积比为( )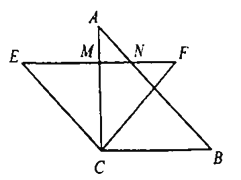
A.
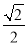 B.
B.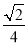 C.
C. D.
D.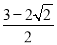
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据阅读材料,解决问题.
数n是一个三位数,各数位上的数字互不相同,且都不为零,从它各数位上的数字中任选两个构成一个两位数,这样就可以得到六个不同的两位数,我们把这六个不同的两位数叫做数n的“生成数”.数n的所有“生成数”之和与22的商记为G(n),例如n=123,它的六个“生成数”是12,13,21,23,31,32,这六个“生成数”的和12+13+21+23+31+32=132,132÷22=6,所以G(123)=6.
(1)计算:G(125),G(746);
(2)数s,t是两个三位数,它们都有“生成数”,a,1,4分别是s的百位、十位、个位上的数字,x,y,6分别是t的百位、十位、个位上的数字,规定:k=
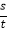 ,若G(s)G(t)=84,求k的最小值.
,若G(s)G(t)=84,求k的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.
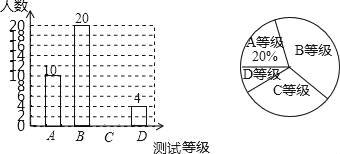
请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生?测试结果为C等级的学生数是 ,并补全条形图;
(2)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两名恰好都是男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点.
(1)a= ,b= ;并在数轴上画出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.

相关试题

