搜索
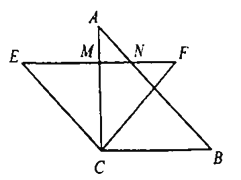
【题目】把两个全等的等腰直角三角形如图放置在一起
，点
关于
对称
交，
于点
，则
与
的面积比为（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】
由轴对称性质得EF⊥AC，由∠A=45°，得出△AMN是等腰直角三角形，由等腰直角三角形的性质得CM=EM=
CE，由△ECF≌△ACB得出AC=CE=BC，则AM=（1-）AC，由等腰直角三角形面积公式即可得出结果．
解：∵△ACB是等腰直角三角形，
∴AC=BC，∠A=45°，
∵点E，F关于AC对称，
∴EF⊥AC，
∵∠A=45°，
∴△AMN是等腰直角三角形，
∵△ECF是等腰直角三角形，
∴CM=EM=
=CE,
∵△ECF≌△ACB，
∴AC=CE=BC，
∴AM=AC-CM=AC-AC=（1-）AC，
∴
=
=
= 
= 
.
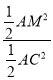故选：D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，德强学校初中部中考屡创佳绩，捷报频传.为了吸纳更多的优质生源，学校决定要新建一栋
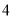层的教学大楼，每层楼有
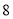间教室，进出这栋大楼共有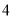道门，其中两道正门大小相同，两道侧门大小相同，进楼前为了保证学生安全，对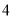道门进行了测试：正常情况下，当同时开启一道正门和两道侧门时，
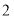分钟可以通过
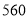名学生；当同时开启一道正门和一道侧门时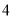分钟可以通过
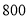名学生.（1）正常情况下，平均每分钟一道正门和一道侧门各可以通过多少名学生？
（2）检查中发现，紧急情况时因学生拥挤，出门的效率将降低
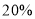，安全检查规定，在紧急情况下全大楼的学生应在
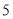分钟内通过这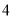道门安全撤离.如果这栋教学楼每班预计招收45名学生，那么建造的这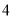道门是否符合安全规定？请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同．甲、乙两人每天共加工35个零件，设甲每天加工x个A型零件．
（1）直接写出乙每天加工的零件个数；（用含x的代数式表示）
（2）求甲、乙每天各加工零件多少个？
（3）根据市场预测，加工A型零件所获得的利润为m元/件（3≤m≤5），加工B型零件所获得的利润每件比A型少1元．求甲、乙每天加工的零件所获得的总利润P（元）与m的函数关系式，并求P的最大值和最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一张长方形纸片，
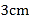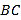长为
，
长为
. 
(1)若将此长方形纸片绕它的一边所在直线旋转一周，则形成的几何体是______；
(2)若将这个长方形纸片绕
边所在直线旋转一周，则形成的几何体的体积是____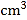
(结果保留
)；(3)若将这个长方形纸片绕它的一边所在直线旋转一周，求形成的几何体的表面积(结果保留
). -
科目： 来源： 题型：
查看答案和解析>>【题目】根据阅读材料，解决问题．
数n是一个三位数，各数位上的数字互不相同，且都不为零，从它各数位上的数字中任选两个构成一个两位数，这样就可以得到六个不同的两位数，我们把这六个不同的两位数叫做数n的“生成数”．数n的所有“生成数”之和与22的商记为G（n），例如n=123，它的六个“生成数”是12，13，21，23，31，32，这六个“生成数”的和12+13+21+23+31+32=132，132÷22=6，所以G（123）=6．
（1）计算：G（125），G（746）；
（2）数s，t是两个三位数，它们都有“生成数”，a，1，4分别是s的百位、十位、个位上的数字，x，y，6分别是t的百位、十位、个位上的数字，规定：k=
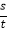，若G（s）G（t）=84，求k的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线y=﹣
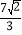x2﹣
x﹣2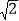
与x轴交于A，B两点（点A在点B的左侧），交y轴于点C．（1）求直线AC的解析式；
（2）点P是直线AC上方抛物线上的一动点，过点P作PD⊥AC，垂足为D，当线段PD的长度最大时，点Q从点P出发，先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处，再沿MC以每秒3个单位的速度运动到点C停止，当点Q在整个运动中所用时间t最少时，求点M的坐标；
（3）如图2，将△BOC沿直线BC平移，平移后B，O，C三点的对应点分别是B′，O′，C′，点S是坐标平面内一点，若以A，C，O′，S为顶点的四边形是菱形，请直接写出所有符合条件的点S的坐标．
-
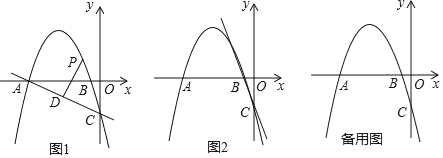
科目： 来源： 题型：
查看答案和解析>>【题目】已知AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K．
（1）如图1，求证：KE=GE；
（2）如图2，连接CABG，若∠FGB=
∠ACH，求证：CA∥FE；（3）如图3，在（2）的条件下，连接CG交AB于点N，若sinE=
，AK=
，求CN的长．
相关试题
