【题目】已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点.
(1)a= ,b= ;并在数轴上画出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.

参考答案:
【答案】(1)4,16;图详见解析;(2)t=![]() 或8;(3)点P和点Q运动4或8或9或11秒时,P,Q两点之间的距离为4,点Q表示的数为20,24,25,27.
或8;(3)点P和点Q运动4或8或9或11秒时,P,Q两点之间的距离为4,点Q表示的数为20,24,25,27.
【解析】
(1)求出a、b的值即可解决问题;
(2)构建方程即可解决问题;
(3)分四种情形构建方程即可解决问题.
(1)∵多项式2x3y﹣xy+16的次数为a,常数项为b,
∴a=4,b=16,
故答案为4,16.
点A、B的位置如图所示.

(2)设运动时间为ts.
由题意:3t=2(16﹣4﹣3t)或3t=2(4+3t﹣16),
解得t=![]() 或8,
或8,
∴运动时间为![]() 或8秒时,点P到点A的距离是点P到点B的距离的2倍;
或8秒时,点P到点A的距离是点P到点B的距离的2倍;
(3)设运动时间为ts.点P在运动开始到结束过程中存在如下符合题意的四种情况:
当点P在A、B之间时,有3t+4=(16-4)+t,解得t=4, 此时点Q表示的数为20;
当点P在B、C之间时,有3t-[(16-4) +t]=t,解得t=8, 此时点Q表示的数为24;
当P到达点C处后返回且Q在P的右侧时,有12+t+4+3t=52,解得t=9,此时点Q表示的数为25;
当P到达终点A,Q继续运动到点C处后返回,并与P相距6时,有12+t+3t﹣4=52,解得t=11,此时点Q表示的数为25.
∴点P和点Q运动4或8或9或11秒时,P,Q两点之间的距离为4.
此时点Q表示的数为20,24,25,27.
-
科目: 来源: 题型:
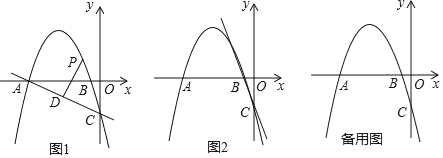
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=﹣
 x2﹣
x2﹣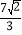 x﹣2
x﹣2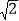 与x轴交于A,B两点(点A在点B的左侧),交y轴于点C.
与x轴交于A,B两点(点A在点B的左侧),交y轴于点C.(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;
(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=
 ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=
 ,AK=
,AK= ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.
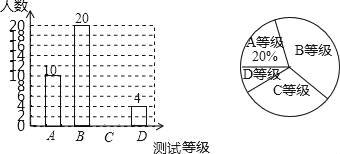
请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生?测试结果为C等级的学生数是 ,并补全条形图;
(2)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两名恰好都是男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正六边形 ABCDEF的中心与坐标原点O重合,其中A(-2,0).将六边形 ABCDEF绕原点O按顺时针方向旋转2018次,每次旋转60°,则旋转后点A的对应点A'的坐标是( ).
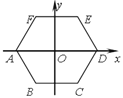
A. (1,
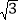 ) B. (
) B. (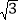 ,1) C. (1,
,1) C. (1,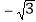 ) D. (-1,
) D. (-1,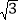 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°将四边形EFCD沿EF翻折,得到四边形EFC’D’,ED’交BC于点G,则△GEF的周长为________.
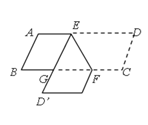
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
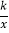 (x>0)经过A、B两点,若点A的横坐标为1,∠OAB=90°,且OA=AB,则k的值为________.
(x>0)经过A、B两点,若点A的横坐标为1,∠OAB=90°,且OA=AB,则k的值为________.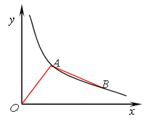
相关试题

