【题目】在我县中小学读书活动中，某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动，将图书分为甲、乙、丙、丁四类，学生可根据自己的爱好任选其中一类，学校根据调查情况进行了统计，并绘制了不完整条形统计图和扇形统计图．

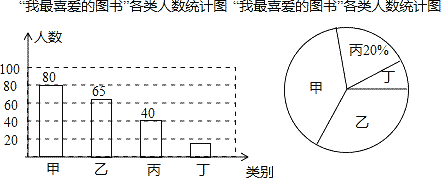
请你结合图中的信息，解答下列问题（其中（1）、（2）直接填答案即可）；

（1）本次调查了　名学生；

（2）被调查的学生中，最喜爱丁类图书的有　　人，最喜爱甲类图书的人数被调查人数的　　%．

（3）在最喜爱丙类图书的学生中，女生人数是男生人数的1.5倍，若这所学校约有学生1800人，请你估计该校最喜爱丙类图书的女生和男生分别有多少人．

参考答案：

【答案】（1）200；（2）15；40；（3）女生和男生分别有216人，144人．

【解析】

（1）根据百分比=频数÷总数可得共调查的学生数；

（2）最喜爱丁类图书的学生数=总数减去喜欢甲、乙、丙三类图书的人数即可；再根据百分比=频数÷总数计算可得最喜爱甲类图书的人数所占百分比；

（3）设男生人数为x人，则女生人数为1.5x人，由题意得方程x+1.5x=1500×20%，解出x的值可得答案．

解：（1）共调查的学生数：

40÷20%=200（人），

故答案为200；

（2）最喜爱丁类图书的学生数：200﹣80﹣65﹣40=15（人）；

最喜爱甲类图书的人数所占百分比：80÷200×100%=40%；

故答案为15；40.

（3）设男生人数为x人，则女生人数为1.5x人，由题意得：

x+1.5x=1800×20%，

解得：x=144，

当x=144时，1.5x=216．

答：该校最喜爱丙类图书的女生和男生分别有216人，144人．

关闭