【题目】如图,△ABC中,AB=AC,△ABD和△ACE分别是以AB、AC为斜边的等腰直角三角形,BE、CD相交于点F.求证:AF⊥BC.

参考答案:
【答案】见解析
【解析】
先证明△ABD≌△ACE,从而有DB=CE,接着证明△DBC≌△ECB,从而∠DCB=∠EBC,所以FB=FC,所以F在BC的垂直平分线上,另A点在BC垂直平分线上,所以AF⊥BC.
证:在△ABD和△ACE中,
∵AB=AC,∠ABD=∠ACE,DB=EC,
∴△ABD≌△ACE.
∴DB=EC.
在△DBC和△ECB中,
∵DB=EC,∠DBC=∠ECB,BC=CB,
∴△DBC≌△ECB.
∴∠DCB=∠EBC,
∴FB=FC.
∴F在BC的垂直平分线上.
又∵另A点在BC垂直平分线上,
∴AF⊥BC.
-
科目: 来源: 题型:
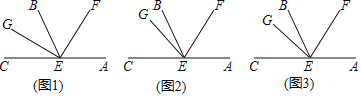
查看答案和解析>>【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是直线AC上一点,EF是∠AEB的平分线.
(1)如图1,若EG是∠BEC的平分线,求∠GEF的度数;
(2)如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.
(3)如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.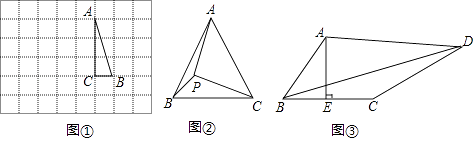
(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
(3)【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
(4)【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2,则a=b;⑥若
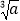 =
= ,则a=b.其中假命题的个数是( )
,则a=b.其中假命题的个数是( )A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.教育主管部门对某学校青年学校青年教师2016年度阅读情况进行了问卷调查,并将收集的数据统计如表,根据表中的信息判断,下列结论错误的是( )

A. 该学校中参与调查的青年教师人数为40人
B. 该学校中青年教师2016年平均每人阅读8本书
C. 该学校中青年教师2016年度看书数量的中位数为4本
D. 该学校中青年教师2016年度看书数量的众数为4本
-
科目: 来源: 题型:
查看答案和解析>>【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

相关试题

