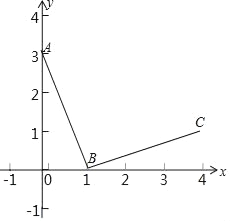
【题目】如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y=![]() 的图象G经过点C.
的图象G经过点C.
(1)请直接写出点C的坐标及k的值;
(2)若点P在图象G上,且∠POB=∠BAO,求点P的坐标;
(3)在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.
参考答案:
【答案】(1)点C的坐标(4,1),k的值是4; (2) P(2![]() ,
,![]() );(3)
);(3) ![]()
【解析】
(1)过C点作CH⊥x轴于H,如图,利用旋转的性质得BA=BC,∠ABC=90°,再证明△ABO≌△BCH得到CH=OB=1,BH=OA=3,则C(4,1),然后把C点坐标代入y=![]() (x>0)中可计算出k的值;
(x>0)中可计算出k的值;
(2)画出过点C的反比例函数y=![]() (x>0)的草图,结合条件点P在图象G上,根据相似三角形的判定和性质即可得到结论;
(x>0)的草图,结合条件点P在图象G上,根据相似三角形的判定和性质即可得到结论;
(3)由Q(0,m),得到OQ=m,得到M(![]() ,m),N(3m,m),根据点M在点N左侧,列不等式即可得到结论.
,m),N(3m,m),根据点M在点N左侧,列不等式即可得到结论.
解:(1) 过C点作CH⊥x轴于H,如图,
∵线段AB绕点B顺时针旋转90°,得到线段BC,
∴BA=BC,∠ABC=90°,
∵∠ABO+∠CBH=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠CBH,
在△ABO和△BCH中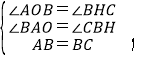
∴△ABO≌△BCH(AAS),
∴CH=OB=1,BH=OA=3,
∴C(4,1),
∵点C落在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=4×1=4;
故答案为:点C的坐标(4,1),k的值是4
(2)过O作OP∥BC交![]() 于点P,过P作PE⊥x轴于E,
于点P,过P作PE⊥x轴于E,
∵∠POE=∠OAB,∠AOB=∠PEO,
∴△OAB∽△OHP,
∴PE:OE=OB:OA=1:3,∵点P在![]() 上
上
∴![]()
![]()
∴P(2![]() ,
,![]() )
)
(3) ![]() ,理由:
,理由:
∵Q(0,m),
∴OQ=m,
∵QM∥x轴,与图象G交于点M,与直线OP交于点N,
∴M(![]() ,m),N(3m,m),
,m),N(3m,m),
∵点M在点N左侧,
∴![]() <3m,
<3m,
∵m>0,
∴m>![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q.已知AC=3cm,BC=6cm,设PC的长度为xcm,BQ的长度为ycm.
小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm
0
0.5
1.0
1.5
2.0
2.5
3
3.5
4
4.5
5
6
y/cm
0
1.56
2.24
2.51
m
2.45
2.24
1.96
1.63
1.26
0.86
0
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y>2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知:⊙O.

求作:⊙O的内接等腰直角三角形.
作法:如图,
①作直径AB;

②分别以点A,B为圆心,以大于
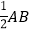 的同样长为半径作弧,两弧交于M,N两点;
的同样长为半径作弧,两弧交于M,N两点;③作直线MN交⊙O于点C,D;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB是直径, C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在测量“河流宽度”的综合与实践活动中,小李同学设计的方案及测量数据如下:在河对岸边选定一个目标点A,在近岸取点B,C,D (点B,C,D在同一条直线上),AB⊥BD,∠ACB=45°,CD=20米,且.若测得∠ADB=25°,请你帮助小李求河的宽度AB.(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,结果精确到0.1米).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是⊙O直径AB上一点,过C作CD⊥AB交⊙O于点D,连接DA,延长BA至点P,连接DP,使∠PDA=∠ADC.
(1)求证:PD是⊙O的切线;
(2)若AC=3,tan∠PDC=
 ,求BC的长.
,求BC的长.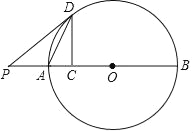
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
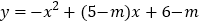 .
.(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线
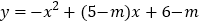 与
与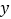 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线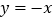 的对称点恰好是点M,求
的对称点恰好是点M,求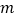 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点E为线段AB上一动点(不与点A,B重合),连接CE,将∠ACE的两边CE,CA分别绕点C顺时针旋转90°,得到射线CE,,CA,,过点A作AB的垂线AD,分别交射线CE,,CA,于点F,G.
(1)依题意补全图形;
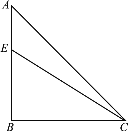
(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示);
(3)用等式表示线段AE,AF与BC之间的数量关系,并证明.
相关试题

