【题目】如图△ABC 中,AC=BC,∠ACB=120°,点 D 在线段 AB 上运动(D 不与 A、B 重合),连接 CD,作∠CDE=30°,DE 交 BC 于点 E,若△CDE 是等腰三角形,则∠ADC 的度数是___________.

参考答案:
【答案】60°或105°
【解析】
分类讨论:当CD=DE时;当DE=CE时;当EC=CD时;然后利用等腰三角形的性质和三角形的内角和定理进行计算.
△CDE可以是等腰三角形,
∵△CDE是等腰三角形;
①当CD=DE时,
∵∠CDE=30°,
∴∠DCE=∠DEC=75°,
∴∠ADC=∠B+∠DCE=105°,
②当DE=CE时,∵∠CDE=30°,
∴∠DCE=∠CDE=30°,
∴∠ADC=∠DCE+∠B=60°.
③当EC=CD时,
∠BCD=180°∠CED∠CDE=180°30°30°=120°
∵∠ACB=180°∠A∠B=120°,
∴此时,点D与点A重合,不合题意.
综上,△ADC可以是等腰三角形,此时∠ADC的度数为60°或105°.
故答案为60°或105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-
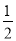 x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
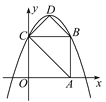
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。(1)求二次函数的解析式;
(2)设二次函数的图象与
 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线
 ,并写出当
,并写出当 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB BC AC,∠A ∠B ∠C 60°.点 D、E 分别是边 AC、AB 上的点(不与 A、B、C 重合),点 P 是平面内一动点.设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点 P 在边 BC 上运动(不与点 B 和点 C 重合),如图⑴所示,则∠1+∠2 .(用 α 的代数式表示)
(2)若点 P 在△ABC 的外部,如图⑵所示,则∠α、∠1、∠2 之间有何关系?写出你的结论,并说明理由.

相关试题

