【题目】如图,已知二次函数![]() 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的解析式;
(2)设二次函数的图象与![]() 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线![]() ,并写出当
,并写出当![]() 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。

参考答案:
【答案】(1)二次函数的解析式为![]()
(2)点D的坐标为(-1,0)
(3)X的取值范围为了-1<x<4
【解析】
试题(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
试题解析:(1)∵函数![]() 图象过点A(2,0)、B(0,1)和C(4,5)三点
图象过点A(2,0)、B(0,1)和C(4,5)三点
∴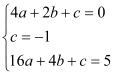 ∴
∴![]()
∴二次函数的解析式为![]()
(2)当Y=0时
得![]()
∴x1=2,x2=-1
∴点D的坐标为(-1,0)
(3)画图正确

X的取值范围为了-1<x<4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-
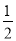 x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
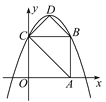
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC 中,AC=BC,∠ACB=120°,点 D 在线段 AB 上运动(D 不与 A、B 重合),连接 CD,作∠CDE=30°,DE 交 BC 于点 E,若△CDE 是等腰三角形,则∠ADC 的度数是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形.

相关试题

