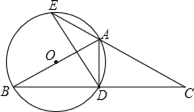
【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
参考答案:
【答案】(1)证明见解析;(2)⊙O的半径为![]() ;(3)AE=
;(3)AE=![]() .
.
【解析】试题分析:(1)根据直径所对的圆周角是直角得到AD⊥BC,应用等腰三角形的三线合一证得点D为BC的中点;
(2)应用等腰三角形的性质和判定证得BD=DE=3,进而求得BD=3,AD=1,应用勾股定理求得AB的长,即可得到半径的长;
(3)解法一:通过证明△CAB∽△CDE,应用相似三角形的性质解得CE的长,再求AE的长;
解法二:连接BE,通过证明△ADC∽△BEC,解得CE的长,再求AE的长.
试题解析:(1)证明:∵AB为⊙O的直径,
∴AD⊥BC,
又∵AB=AC,
∴D是BC的中点.
(2)解:∵AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠C=∠E,则DC=DE,
∴BD=DE=3,
又BD-AD=2,
∴AD=1,
在Rt△ABD中,BD=3,AD=1,
∴AB=![]() ,
,
则⊙O的半径为![]() .
.
(3)解法一:在△CAB和△CDE中,
∠B=∠E,∠C=∠C(公共角),
∴△CAB∽△CDE,
∴![]() ,
,
∵CA=AB=![]() ,
,
∴![]() ,
,
∴AE=CE-AC=![]() =
=![]() .
.
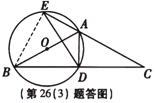
解法二:连接BE,
∵AB为⊙O的直径,
∴∠BEC=![]() ,
,
在△ADC和△BEC中,
∠ADC=∠BEC=![]() ,∠C=∠C,
,∠C=∠C,
∴△ADC∽△BEC,
∴![]() ,
,
∴![]() ,
,
∴AE=CE-AC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:

(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适宜采用全面调查方式(普查)的是( )
A. 对襄阳市中学生每天课外读书所用时间的调查
B. 对全国中学生心理健康现状的调查
C. 对七年级(2)班学生
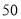 米跑步成绩的调查
米跑步成绩的调查D. 对市面某品牌中性笔笔芯使用寿命的调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
-
科目: 来源: 题型:
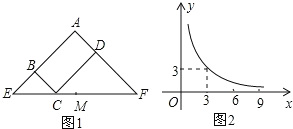
查看答案和解析>>【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
相关试题

