【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F. 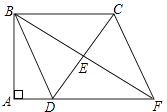
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
参考答案:
【答案】
(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
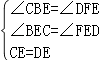 ,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)解:①BC=BD=3时,由勾股定理得,AB= ![]() =
= ![]() =2
=2 ![]() ,
,
所以,四边形BDFC的面积=3×2 ![]() =6
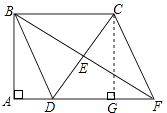
=6 ![]() ;②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG=
;②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG= ![]() =
= ![]() =
= ![]() ,所以,四边形BDFC的面积=3×
,所以,四边形BDFC的面积=3× ![]() =3
=3 ![]() ;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;综上所述,四边形BDFC的面积是6
;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;综上所述,四边形BDFC的面积是6 ![]() 或3
或3 ![]() .
.
【解析】(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;(2)分①BC=BD时,利用勾股定理列式求出AB,然后利用平行四边形的面积公式列式计算即可得解;②BC=CD时,过点C作CG⊥AF于G,判断出四边形AGCB是矩形,再根据矩形的对边相等可得AG=BC=3,然后求出DG=2,利用勾股定理列式求出CG,然后利用平行四边形的面积列式计算即可得解;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A和点B表示的教分别为﹣4和2,把点A向右平移( )个单位长度,可以使点A到点B的距离是2.
A. 2或4 B. 4或6 C. 6或8 D. 4或8
-
科目: 来源: 题型:
查看答案和解析>>【题目】设计一张折叠型方桌子如图,若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( )
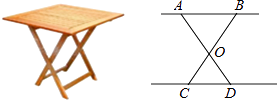
A.60°
B.90°
C.120°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)3a2(﹣2a3)
(2)
(3)9(x+2)(x﹣2)﹣(3x﹣2)2
(4)(2m+n﹣p)(2m﹣n+p) -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AD、AE分别为角平分线和高,若∠B=60°,∠C=70°,求∠DAE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克
0
1
2
3
4
5
弹簧的长度/厘米
10
10.4
10.8
11.2
11.6
12
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2,3,﹣4,﹣5,6这五个数中任取两个数相乘,其积最大是_____.
相关试题

