【题目】△ABC中,AD、AE分别为角平分线和高,若∠B=60°,∠C=70°,求∠DAE. 
参考答案:
【答案】解:在△ABC中,∵AD平分∠BAC, ∴∠CAD= ![]() ∠BAC,
∠BAC,
∵∠B=60°,∠C=70°,
∴∠BAC=50°,∠DAC=25°,
∵AE⊥BC,∠C=70°,
∴∠EAC=20°
∴∠DAE=∠CAD﹣∠EAC=5°
【解析】根据三角形内角和定理求得∠BAC的度数,则根据角平分线的定义求得角∠DAC,然后在直角△ACE中,求得∠EAC的度数,则∠DAE=∠CAD﹣∠EAC即可求解.
【考点精析】掌握三角形的“三线”和三角形的内角和外角是解答本题的根本,需要知道1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设计一张折叠型方桌子如图,若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( )
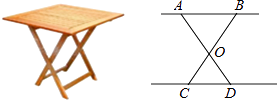
A.60°
B.90°
C.120°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)3a2(﹣2a3)
(2)
(3)9(x+2)(x﹣2)﹣(3x﹣2)2
(4)(2m+n﹣p)(2m﹣n+p) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
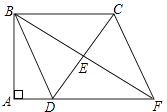
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克
0
1
2
3
4
5
弹簧的长度/厘米
10
10.4
10.8
11.2
11.6
12
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2,3,﹣4,﹣5,6这五个数中任取两个数相乘,其积最大是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 2b2﹣b2=1 B. 2a2+3a3=5a5
C. 2a+3b=5ab D. 4a2b+ba2=5a2b
相关试题

