【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
参考答案:
【答案】
(1)
解:如图,判断3正确.理由如下:
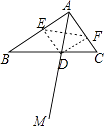
∵∠BAC=90°,DE⊥ABDF⊥AC,
∴DE=DF,∴∠AED=∠AFD=∠EAF=90°,
∴四边形AEDF是矩形,∵DE=DF,
∴四边形AEDF是正方形,
∴AD与EF互相垂直平分.
故判断3正确
(2)
解:①结论:△BCN是等腰直角三角形.理由如下:
如图作NE⊥AB于E,FN⊥AC于F.
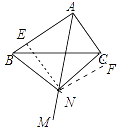
∵MA是∠BAC的平分线,
∴NE=NF,
在Rt△NEB和Rt△NFC中,
![]() ,
,
∴△NEB≌△NFC,
∴BE=CF,∠BNE=∠CNF,
易知四边形AENF是正方形,
∴AE=AF,∠BNC=∠ENF=90°,
∴△BNC是等腰直角三角形.
②∵AB+AC=(AE+BE)+(AF﹣CF)=2AE=18,
∴AE=AF=9,
∵△NEB≌△NFC,
∴S△NEB=S△NFC,
∴S四边形ABNC=S正方形AENF=92=81
【解析】(1)结论:判断3正确.只要证明四边形AEDF是正方形即可解决问题.(2)①△BCN是等腰直角三角形.如图作NE⊥AB于E,FN⊥AC于F.只要证明△NEB≌△NFC,四边形AENF是正方形即可解决问题.②由△NEB≌△NFC,推出S△NEB=S△NFC , 推出S四边形ABNC=S正方形AENF , 由此即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班去体育用品商店购买羽毛球和羽毛球拍,每只羽毛球2元,每副羽毛球拍25元.甲商店说:“羽毛球拍和羽毛球都打9折优惠”,乙商店说:“买一副羽毛球拍赠2只羽毛球”.
(1)该班如果买2副羽毛球拍和20只羽毛球,问在甲、乙两家商店各需花多少钱?
(2)该班如果准备花90元钱全部用于买2副羽毛球拍和若干只羽毛球,请问到哪家商店购买更合算?
(3)该班如果必须买2副羽毛球拍,问当买多少只羽毛球时到两家商店购买同样合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知10a=5,10b=6,求102a+3b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知今年小明的年龄是
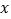 岁,小红的年龄比小明的2倍少4岁,小华的年龄比小红的
岁,小红的年龄比小明的2倍少4岁,小华的年龄比小红的 还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含
还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含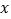 的式子表示小刚的年龄,并计算当
的式子表示小刚的年龄,并计算当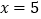 时小刚的年龄.
时小刚的年龄. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市2018年的最高气温为30℃,最低气温为零下18℃,则计算2018年的温差是( )
A.12℃B.48℃C.﹣12℃D.﹣48℃
-
科目: 来源: 题型:
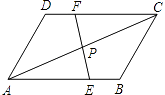
查看答案和解析>>【题目】已知:点P是ABCD的对角线AC的中点,经过点P的直线EF交AB于点E,交DC于点F.求证:AE=CF.
-
科目: 来源: 题型:
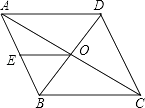
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,已知AC=8cm,BD=6cm,求OE的长.
相关试题

