【题目】如图,菱形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,已知AC=8cm,BD=6cm,求OE的长. 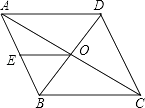
参考答案:
【答案】解:∵ABCD是菱形 ∴OA=OC,OB=OD,OB⊥OC
又∵AC=8cm,BD=6cm
∴OA=OC=4cm,OB=OD=3cm
在直角△BOC中,
由勾股定理,得BC= ![]() =5cm
=5cm
∵点E是AB的中点
∴OE是△ABC的中位线,
∴OE= ![]() cm.
cm.
【解析】根据菱形的性质及中位线定理解答.
【考点精析】本题主要考查了勾股定理的概念和三角形中位线定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.

(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市2018年的最高气温为30℃,最低气温为零下18℃,则计算2018年的温差是( )
A.12℃B.48℃C.﹣12℃D.﹣48℃
-
科目: 来源: 题型:
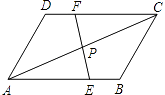
查看答案和解析>>【题目】已知:点P是ABCD的对角线AC的中点,经过点P的直线EF交AB于点E,交DC于点F.求证:AE=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:
挪动珠子数(颗)
2
3
4
5
6
…
所得分数(分)
5
11
19
29
41
…
按表中规律,当所得分数为71时,则挪动的珠子数为_____颗;当挪动n颗珠子时(n为大于1的整数),所得分数为_______(用含n的代数式表示)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a﹣3b=7,则8+6b﹣4a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂今年3月的产值为50万元,5月份上升到72万元,这两个月平均每月增长的百分率是多少?若设平均每月增长的百分率为x,则列出的方程正确的是( )
A.50(1+x)=72B.50(1+x)+50(1+x)2=72
C.50(1+x)×2=72D.50(1+x)2=72
相关试题

