搜索
【题目】把某不等式组中两个不等式的解集表示在数轴上，如图所示，则这个不等式组可能是 ( )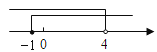
A.
B.
C.
D.
参考答案：
【答案】B
【解析】本题根据数轴可知x的取值为：-1≤x＜4，将不等式变形，即可得出关于x的不等式组．把各个选项的解的集合写出，进行比较就可以得到．
依题意得这个不等式组的解集是：-1≤x＜4．
A、
无解，故A错误；
B、
解集是：-1≤x＜4，故B正确；
C、
解集是：x＞4，故C错误；
D、
解集是：-1＜x≤4，故D错误；
故选：B．
【考点精析】利用不等式的解集在数轴上的表示对题目进行判断即可得到答案，需要熟知不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈．
-
科目： 来源： 题型：
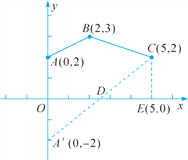
查看答案和解析>>【题目】如图，某公路(可视为x轴)的同一侧有A，B，C三个村庄，要在公路边建一货仓D，向A，B，C三个村庄送农用物资，路线是D→A→B→C→D.
(1)试问：在公路边是否存在一点D，使送货路程最短？
(2)求出点D的坐标，并说明理由．
-
科目： 来源： 题型：
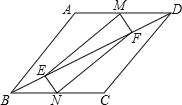
查看答案和解析>>【题目】如图，已知平行四边形ABCD，点M，N分别在边AD和边BC上，点E，F在线段BD上，且AM=CN，DF=BE．求证：
（1）∠DFM=∠BEN；
（2）四边形MENF是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知y1关于x的二次函数y1=ax2+bx+c（a≠0）的图象过点（0，1），且在y轴的左侧，函数值y1随着自变量x的增大而增大．
（1）填空：a 0，b 0，c 0（用不等号连接）；
（2）已知一次函数y2=ax+b，当﹣1≤x≤1时，y2的最小值为﹣
且y1≤1，求y1关于x的函数解析式；（3）设二次函数y1=ax2+bx+c的图象与x轴的一个交点为（﹣1，0），且当a≠﹣1时，一次函数y3=2cx+b﹣a与y4=
x﹣c（m≠0）的图象在第一象限内没有交点，求m的取值范围． -
科目： 来源： 题型：
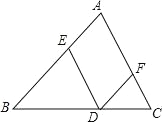
查看答案和解析>>【题目】已知D为△ABC边BC上的一个动点（不与B，C重合），过D作DE∥AC交AB于点E，作DF∥AB交AC于点F．
（1）证明：△BDE∽△DCF；
（2）若△ABC的面积为10，点G为线段AF上的任意一点，设FC：AC=n，△DEG的面积为S，求S关于n的关系式，并求S的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P（a+1，﹣
+1）关于原点对称的点在第四象限，则a的取值范围在数轴上表示正确的是（ ）
A.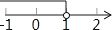
B.
C.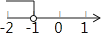
D.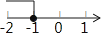
-
科目： 来源： 题型：
查看答案和解析>>【题目】不等式组
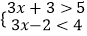的解集在数轴上的表示是（ ）
A.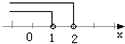
B.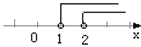
C.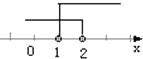
D.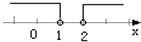
相关试题
