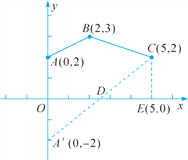
【题目】如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货仓D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D.
(1)试问:在公路边是否存在一点D,使送货路程最短?
(2)求出点D的坐标,并说明理由.
参考答案:
【答案】(1)存在(2)(![]() ,0)
,0)
【解析】试题分析:本题考查最短路线问题,因为路程即为DA+AB+BC+DC,AB+BC的长度固定,所以要使路程最短,只需DA+DC最短即可,根据小马饮水问题的解决方法可知,作点A关于x轴对称的点A′,然后连接A′C, A′C与x轴的交点即为点D, A′C即为DA+DC最短距离,根据待定系数法求A′C的直线解析式,再求直线与x轴的交点.
(1)存在.
(2)∵路程即为DA+AB+BC+DC,AB+BC的长度固定,∴要使路程最短,只需DA+DC最短即可.
作点A关于x轴的对称点A′(0,-2),连结A′C,则A′C与x轴的交点即为点D.
过点C作CE⊥x轴于点E,则点E(5,0),易得△OA′D≌△ECD,得OD=ED,∴点D![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
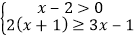 并把解集在数轴上表示出来.
并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个点中在函数y=2x-3的图象上有( )个.
(1,2) , (3,3) , (-1, -1), (1.5,0)
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
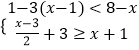 ,并在数轴上表示出其解集.
,并在数轴上表示出其解集. -
科目: 来源: 题型:
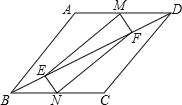
查看答案和解析>>【题目】如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知y1关于x的二次函数y1=ax2+bx+c(a≠0)的图象过点(0,1),且在y轴的左侧,函数值y1随着自变量x的增大而增大.
(1)填空:a 0,b 0,c 0(用不等号连接);
(2)已知一次函数y2=ax+b,当﹣1≤x≤1时,y2的最小值为﹣
 且y1≤1,求y1关于x的函数解析式;
且y1≤1,求y1关于x的函数解析式;(3)设二次函数y1=ax2+bx+c的图象与x轴的一个交点为(﹣1,0),且当a≠﹣1时,一次函数y3=2cx+b﹣a与y4=
 x﹣c(m≠0)的图象在第一象限内没有交点,求m的取值范围.
x﹣c(m≠0)的图象在第一象限内没有交点,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是 ( )
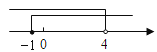
A.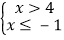
B.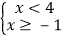
C.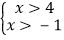
D.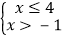
相关试题

