【题目】“世界杯”期间,某娱乐场所举办“消夏看球赛”活动,需要对会场进行布置,计划在现场安装小彩灯和大彩灯.已知安装5个小彩灯和4个大彩灯共需150元;安装7个小彩灯和6个大彩灯共需220元.
(1)安装1个小彩灯和1个大彩灯各需多少元?
(2)若场地共需安装小彩灯和大彩灯300个,费用不超过4350元,则最多安装大彩灯多少个?
参考答案:
【答案】(1) 每个小彩灯10元,每个大彩灯25元;(2) 90个.
【解析】
(1)设小彩灯每个x元,大彩灯每个y 元,根据等量关系:①安装5个小彩灯和4个大彩灯共需150元;②安装7个小彩灯和6个大彩灯共需220元列出二元一次方程组,解方程组即可求得所求答案;
(2)设安装a个大彩灯,则小彩灯安装(300-a)个,根据两种彩灯安装总费用不超过4350元列出不等式,解不等式求得其最大整数解,即可得到所求答案.
(1)解:设小彩灯每个x元,大彩灯每个y 元,根据题意得:
![]() ,解得
,解得![]() .
.
答:每个小彩灯10元,每个大彩灯25元.
(2)设安装a个大彩灯,则安装(300-a)个小彩灯,根据题意可得:
10(300-a)+25a≤4350,
解得:a≤90,
∴a的最大整数解为90.
∴最多安装90个大彩灯.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD,点F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 度;
(2)判断△BEF的形状为 ;
(3)若∠BFC=90°,说明AE∥BF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2m n+n2)+( )=0,
即( )2+( )2=0.根据非负数的性质,
∴m=n=
完善上述解答过程,然后解答下面的问题:
设等腰三角形ABC的三边长a、b、c,且满足a2+b2-4a-6b+13=0,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
-
科目: 来源: 题型:
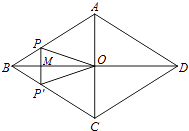
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A.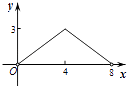
B.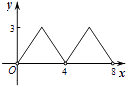
C.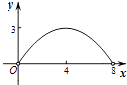
D.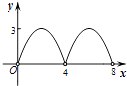
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

相关试题

