【题目】如图,正方形ABCD,点F为正方形ABCD内一点,△BFC逆时针旋转后能与△BEA重合.
(1)旋转中心是点 ,旋转角度为 度;
(2)判断△BEF的形状为 ;
(3)若∠BFC=90°,说明AE∥BF.

参考答案:
【答案】(1)点B, 90°;(2) 等腰直角三角形 ;(3)见解析.
【解析】
(1)根据旋转的定义结合已知条件分析解答即可;
(2)由旋转的性质可知,BE=BF,∠EBF=∠ABC=90°,由此可得△BEF是等腰直角三角形;
(3)由∠BFC=90°可得∠FBC+∠FCB=90°,结合∠FBC+∠ABF=90°,可得∠ABF=∠FCB,由旋转的性质可得∠EAB=∠FCB,由此可得∠EAB=∠ABF,从而可得AE∥BF.
(1)如图所示,∵△BFC经逆时针旋转后能与△BEA重合,
∴旋转中心是点B,∠EBF和∠ABC是旋转角,
∵四边形ABCD是正方形,
∴∠ABC=90°,即旋转角为90°;
(2)△BEF是等腰直角三角形.理由如下:
∵△BFC经逆时针旋转后能与△BEA重合,
∴∠EBF=∠ABC,BF=BE.
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠EBF=90°,
∴△BEF是等腰直角三角形;
(3)∵在△BFC中,∠BFC=90°,
∴∠FBC+∠FCB=90°,
又∵∠FBC+∠ABF=∠EBF=90°,
∴∠ABF=∠FCB,
∵△BEF是由△BFC绕点B旋转形成的,
∴∠EAB=∠FCB,
∴∠EAB=∠ABF,
∴AE∥BF.
-
科目: 来源: 题型:
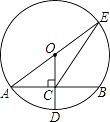
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2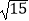
B.8
C.2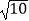
D.2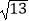
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )

A.40°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;
(2)画出该函数的图象;
(3)判断点(3,5)是否在此函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2m n+n2)+( )=0,
即( )2+( )2=0.根据非负数的性质,
∴m=n=
完善上述解答过程,然后解答下面的问题:
设等腰三角形ABC的三边长a、b、c,且满足a2+b2-4a-6b+13=0,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界杯”期间,某娱乐场所举办“消夏看球赛”活动,需要对会场进行布置,计划在现场安装小彩灯和大彩灯.已知安装5个小彩灯和4个大彩灯共需150元;安装7个小彩灯和6个大彩灯共需220元.
(1)安装1个小彩灯和1个大彩灯各需多少元?
(2)若场地共需安装小彩灯和大彩灯300个,费用不超过4350元,则最多安装大彩灯多少个?
相关试题

