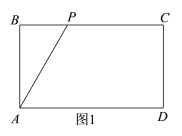
【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

参考答案:
【答案】(1)当t=10,点p到点C,当t=20,点p到点A;(2)10≤t≤14;(3)t=5.5或t=18.5; (4)t=![]() 或 t=7.
或 t=7.
【解析】
(1)根据长方形ABCD的边长和点P的运动速度进行计算即可;
(2)由图可知,当点P在边CD上运动时,△ABP的面积最大,由此根据已知条件计算出点P在边CD上运动所对应的时间范围即可;
(3)如图1和图2,分点P在BC上和AD上两种情况结合已知条件解答即可;
(4)由题意可知,点P、Q在长方形ABCD上从A点出发,作相向运动,因此存在以下两种情况: ①点P、Q相遇前相距1个单位长度,如下图3所示;②点P、Q相遇后相距1个单位长度,如下图4所示;结合已知条件分这两种情况解答即可.
(1)∵AD=BC=6,AB=CD=4,
∴AB+BC=10,AB+BC+CD+DA=20,
又∵点P的移动速度为每秒1个单位长度,
∴点P由A到C所需时间为:10÷1=10(秒),
点P由A出发回到A所需时间为:20÷1=20(秒);
(2)由图可知,当点P在边CD上运动时,△ABP的面积最大,
∵AB+BC+CD=14,
∴点P移动到点D的时间为:14÷1=14(秒),
又∵点P移动到点C的时间为10秒,
∴当△ABP的面积最大时,![]() ;
;
(3)①如图1,当点P在边BC上时,由已知可得:AB=4,PB=(t-4),由题意可得:
S△ABP=![]() ,解得:
,解得:![]() ;
;
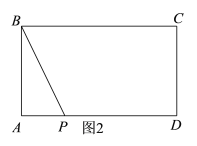
②如图2,当点P在边AD上时,由已知可得:AB=4,AP=(20-t),由题意可得:S△ABP=![]() ,解得:
,解得:![]() ,
,
综上所述,当t=5.5或t=18.5时,△ABP的面积为3.
(4)①如图3,当点P、Q相遇前相距1个单位长度时,
由题意可得:![]() ,解得:
,解得:![]() ;
;

②如图4,当点P、Q在相遇后相距1个单位长度时,由题意可得:
![]() ,解得:
,解得:![]() ,
,

综上所述,当![]() 或
或![]() 时,点P、Q在长方形ABCD的边上相距1个单位长度.
时,点P、Q在长方形ABCD的边上相距1个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界杯”期间,某娱乐场所举办“消夏看球赛”活动,需要对会场进行布置,计划在现场安装小彩灯和大彩灯.已知安装5个小彩灯和4个大彩灯共需150元;安装7个小彩灯和6个大彩灯共需220元.
(1)安装1个小彩灯和1个大彩灯各需多少元?
(2)若场地共需安装小彩灯和大彩灯300个,费用不超过4350元,则最多安装大彩灯多少个?
-
科目: 来源: 题型:
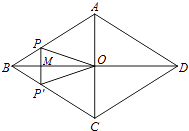
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A.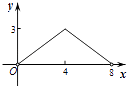
B.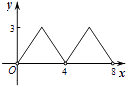
C.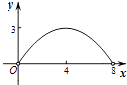
D.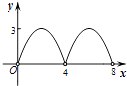
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+
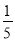 a2b+3,B=﹣
a2b+3,B=﹣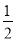 a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣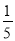 (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.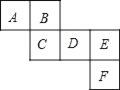
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(-2,0) ,B(-1,2) ,C(1,0) ,连接 AB,点 D 为 AB 的中点,连接 OB 交 CD于点 E,则四边形 DAOE 的面积为( )
A. 1. B.
 C.
C. 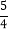 D.
D. 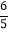
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A第,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
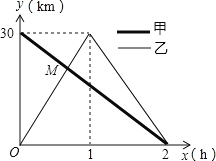
(1)A、B两地之间的距离: km;
(2)甲的速度为 km/h;乙的速度为30km/h;
(3)点M的坐标为 ;
(4)求:甲离B地的距离y(km)与行驶时间x(h)之间的函数关系式(不必写出自变量的取值范围).
相关试题

