【题目】问题情境
学习完本册第二章“轴对称图形”后,张老师在课堂上提出这样的问题:“如图①,在△ABC中,∠A=30°,∠B=60°,如何画一条线段把△ABC分割成两个等腰三角形?”请在图中画出这条线段,并标出相关的度数.
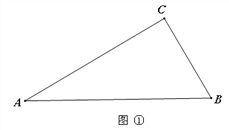
问题探究
探究一:课后,小华经过探究发现:如图②,在△ABC中,∠A=26°,∠B=52°,也可以画一条线段把△ABC分割成两个等腰三角形.请在图中画出这条线段,并标出相关的度数.
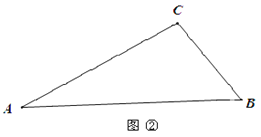
探究二:如图③,在△ABC中,当,∠B=2∠A时,是否一定存在一条线段把△ABC分割成两个等腰三角形?若能,请在图中画出这条线段,若不能,直接写出∠A的取值范围.
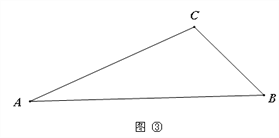
参考答案:
【答案】见解析
【解析】试题分析:本题考查等腰三角形的构造方法,根据垂直平分线上的点到线段两端点距离相等,则以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A,然后再根据等角对等边来判定是否为等腰三角形.
以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A=60°,
因为∠B=60°,所以∠CDB=∠B,所以△BDC是等腰三角形.
以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A=52°,
因为∠B=52°,所以∠CDB=∠B,所以△BDC是等腰三角形.
以线段AC为底,作线段AC的垂直平分线交线段AB于一点D,连接DC,则△ADC是等腰三角形,再根据三角形的外角性质可知∠CDB=2∠A= ![]() ,
,
根据等腰三角形的性质和三角形内角和性质得, ![]() ,
, ![]() ,所以
,所以![]() ,
,
所以当![]() 时,通过作线段AC的垂直平分线交线段AB于一点D,连接DC,可将
时,通过作线段AC的垂直平分线交线段AB于一点D,连接DC,可将
△ABC分为两个等腰三角形.
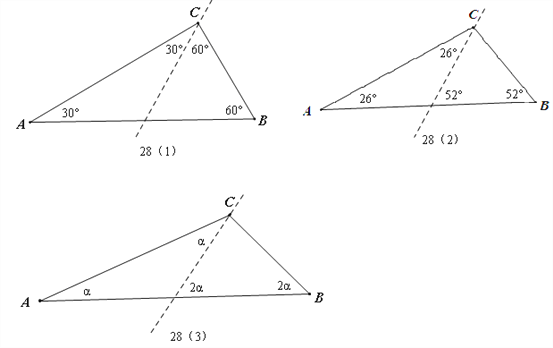
探究一:如图28(2)
探究二:设∠A=α则,∠B=2α如图28(3),0°<∠A<45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论错误的是
A. 全等三角形对应边上的中线相等
B. 两个直角三角形中,两个锐角相等,则这两个三角形全等
C. 全等三角形对应边上的高相等
D. 两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3b﹣4ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )
A.600m2
B.625m2
C.650m2
D.675m2 -
科目: 来源: 题型:
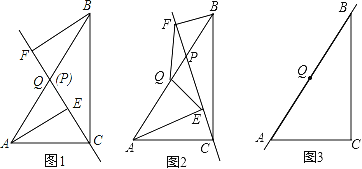
查看答案和解析>>【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
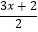 <x的解集是 ( )
<x的解集是 ( )
A.x<-2
B.x<-1
C.x<0
D.x>2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.x3+x2=x5B.x3-x2=xC.(x3)3=x6D.x3·x2=x5
相关试题

