【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
参考答案:
【答案】(1)y1=2x(x≥0);y=![]() x2(x≥0);(2)当x=8时,z的最大值是32.
x2(x≥0);(2)当x=8时,z的最大值是32.
【解析】
试题分析:(1)可根据图象利用待定系数法求解函数解析式;
(2)根据总利润=树木利润+花卉利润,列出函数关系式,再求函数的最值.
试题解析:(1)设y1=kx,由图①所示,函数y1=kx的图象过(1,2),
所以2=k1,k=2,
故利润y1关于投资量x的函数关系式是y1=2x(x≥0);
∵该抛物线的顶点是原点,
∴设y2=ax2,
由图②所示,函数y2=ax2的图象过(2,2),
∴2=a22,a=![]() ,
,
故利润y2关于投资量x的函数关系式是:y=![]() x2(x≥0);
x2(x≥0);
(2)设这位专业户投入种植花卉x万元(0≤x≤8),则投入种植树木(8-x)万元,他获得的利润是z
元,根据题意,
得z=2(8-x)+![]() x2=
x2=![]() x2-2x+16=
x2-2x+16=![]() (x-2)2+14,
(x-2)2+14,
当x=2时,z的最小值是14,
∵0≤x≤8,
∴-2≤x-2≤6,
∴(x-2)2≤36,
∴![]() (x-2)2≤18,
(x-2)2≤18,
∴![]() (x-2)2+14≤18+14=32,
(x-2)2+14≤18+14=32,
即z≤32,此时x=8,
答:当x=8时,z的最大值是32.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
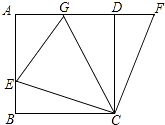
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2
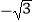 2013×
2013× 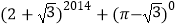 +|
+| 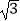 ﹣2|+9×3﹣2 .
﹣2|+9×3﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形的两条对角线长为8cm和6cm,那么这个菱形的周长是cm,面积是cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
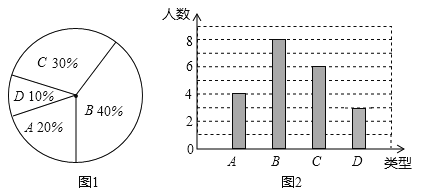
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小王是这样分析的:

① 小王的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣3x=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线
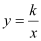 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.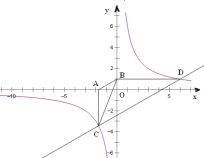
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
相关试题

