【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 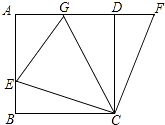
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
参考答案:
【答案】
(1)证明:在正方形ABCD中,
∵ 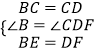 ,
,
∴△CBE≌△CDF(SAS).
∴CE=CF
(2)解:GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵ 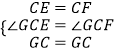 ,
,
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
【解析】(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC两边的长分别是一元二次方程x2﹣5x+6=0的两个解,则这个等腰三角形的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+4x+m-1=0。
(1)当m何值时,方程有两个相等的实数根;
(2)当m=2时,设α、β是方程的两个实数根,求α2+β2+αβ的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,菱形花坛ABCD周长是80m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,相交于O点.
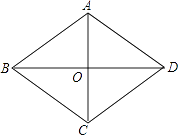
(1)求两条小路的长AC、BD.(结果可用根号表示)
(2)求花坛的面积.(结果可用根号表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2
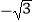 2013×
2013× 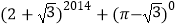 +|
+| 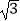 ﹣2|+9×3﹣2 .
﹣2|+9×3﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形的两条对角线长为8cm和6cm,那么这个菱形的周长是cm,面积是cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润
 与投资量
与投资量 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润 与投资量
与投资量 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
(1)分别求出利润
 与
与 关于投资量
关于投资量 的函数关系式;
的函数关系式;(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
相关试题

