【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
参考答案:
【答案】
(1)解:甲: ![]() ×(74+58+87)=
×(74+58+87)= ![]() ×219=73,
×219=73,
乙: ![]() ×(87+74+43)=
×(87+74+43)= ![]() ×204=68,
×204=68,
丙: ![]() ×(69+70+65)=
×(69+70+65)= ![]() ×204=68,
×204=68,
∵73分最高,
∴应该录取甲
(2)解:甲: ![]() ×(74×4+58×3+87×1)=
×(74×4+58×3+87×1)= ![]() ×557=69.625,
×557=69.625,
乙: ![]() ×(87×4+74×3+43×1)=
×(87×4+74×3+43×1)= ![]() ×613=76.625,
×613=76.625,
丙: ![]() ×(69×4+70×3+65×1)=
×(69×4+70×3+65×1)= ![]() ×551=68.875,
×551=68.875,
∵76.625分最高,
∴应该录取乙
【解析】(1)根据算术平均数的计算方法分别求出三人的平均分,然后作出判断即可;(2)根据加权平均数的计算方法分别求出三人的平均分,然后作出判断即可.
【考点精析】解答此题的关键在于理解算术平均数的相关知识,掌握总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得 ,(x、y为正整数)∴
,(x、y为正整数)∴ 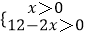 则有0<x<6.又
则有0<x<6.又  为正整数,则
为正整数,则  为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 .
.
∴2x+3y=12的正整数解为
问题:
(1)请你写出方程2x+y=5的一组正整数解
(2)若 为自然数,则满足条件的x值有( )个;
为自然数,则满足条件的x值有( )个;
A.2
B.3
C.4
D.5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解方程
(1)计算:(﹣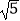 )2+(
)2+( 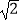 +1)(
+1)( 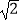 ﹣1)﹣
﹣1)﹣ 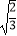 ×
× 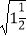
(2)解方程:x2﹣2x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.

(1)(i)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为 ,且点B在格点上. (ii)以上题所画的线段AB为一边,另外两条边长分别为
,且点B在格点上. (ii)以上题所画的线段AB为一边,另外两条边长分别为  ,
,  .画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
.画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
(2)所画出的△ABC的边AB上的高线长为 . (直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.在数轴上表示-a的点一定在原点的左边
B.有理数a的倒数是
C.一个数的相反数一定小于或等于这个数
D.如果一个数的绝对值等于这个数的相反数,那么这个数是负数或零
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形.
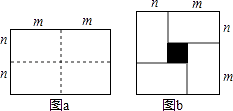
(1)图b中的阴影部分面积为;
(2)观察图b,请你写出三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是;
(3)若x+y=﹣6,xy=2.75,利用(2)提供的等量关系计算x﹣y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(-1,0),A点的横坐标是2,AB=3BC,双曲线
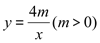 经过A点,双曲线y=-
经过A点,双曲线y=-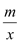 经过C点,则Rt△ABC的面积为_________。
经过C点,则Rt△ABC的面积为_________。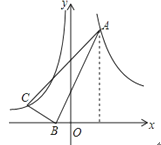
相关试题

