【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得 ![]() ,(x、y为正整数)∴
,(x、y为正整数)∴ ![]() 则有0<x<6.又
则有0<x<6.又 ![]() 为正整数,则
为正整数,则 ![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 ![]() .
.
∴2x+3y=12的正整数解为 ![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解
(2)若 ![]() 为自然数,则满足条件的x值有( )个;
为自然数,则满足条件的x值有( )个;
A.2
B.3
C.4
D.5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
参考答案:
【答案】
(1)
解:由2x+y=5,得y=5﹣2x(x、y为正整数).
所以 ![]() ,即0<x<
,即0<x< ![]()
∴当x=1时,y=3;
当x=2时,y=1.
即方程的正整数解是 ![]() 或
或 ![]() .(只要写出其中的一组即可)
.(只要写出其中的一组即可)
(2)C
(3)
解:设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=35,其中m、n均为自然数.
于是有: ![]() ,
,
解得: 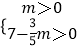 ,
,
所以0<m< ![]() .
.
由于n=7﹣ ![]() m为正整数,则
m为正整数,则 ![]() 为正整数,可知m为5的倍数.
为正整数,可知m为5的倍数.
∴当m=5时,n=4;
当m=10时,n=1.
答:有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;
或购买单价为3元的笔记本10本,单价为5元的钢笔1支
【解析】解:(2)同样,若 ![]() 为自然数,
为自然数,
则有:0<x﹣2≤6,即2<x≤8.
当x=3时, ![]() ;
;
当x=4时, ![]() ;
;
当x=5时, ![]() ;
;
当x=8时, ![]() .
.
即满足条件x的值有4个,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,图表和图是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:

频率分布表
器材种类
频数
频率
排 球
20
乒乓球拍
50
0.50
篮 球
25
0.25
足 球
合 计
1
(1)填充频率分布表中的空格.
(2)在图中,将表示“排球”和“足球”的部分补充完整.
(3)若该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元,现根据筹备实际需要,准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】把﹣1﹣(+4)﹣(﹣3)+(﹣6)+(+2)写成省略加号的和的形式,正确的是( )
A. ﹣1﹣4﹣3﹣6+2 B. ﹣1+4+3﹣6+2 C. ﹣1﹣4+3﹣6+2 D. ﹣1﹣4﹣3+6+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为完成下列任务,你认为采用什么调查方式最合适?
(1)了解某市居民的年人均收入;
(2)了解某班学生期末考试的数学成绩;
(3)了解一个月内某城市一条道路的车流量;
(4)了解某电视台一个娱乐节目的收视率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解方程
(1)计算:(﹣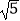 )2+(
)2+( 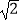 +1)(
+1)( 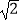 ﹣1)﹣
﹣1)﹣ 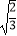 ×
× 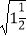
(2)解方程:x2﹣2x﹣1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.

(1)(i)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为 ,且点B在格点上. (ii)以上题所画的线段AB为一边,另外两条边长分别为
,且点B在格点上. (ii)以上题所画的线段AB为一边,另外两条边长分别为  ,
,  .画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
.画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
(2)所画出的△ABC的边AB上的高线长为 . (直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人
测试成绩
题目
甲
乙
丙
文化课知识
74
87
69
面试
58
74
70
平时表现
87
43
65
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?
相关试题

