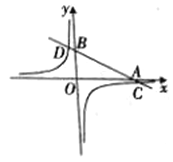
【题目】如图,在平面直角坐标系中,一次函数y= kx +b(k≠0)的图象分别交x轴、y轴于A、B两点,与反比例函数y=![]() (m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(1)求m的值和点D的坐标;
(2)求线段AB的长度;
(3)根据图象直接写出: 当x为何值时,一次函数的值大于反比例函数的值?
参考答案:
【答案】(1)m=-6,D(-2,3);(2)2![]() ;(3)<-2或0<x<6.
;(3)<-2或0<x<6.
【解析】
(1)根据函数图象上的点的坐标即可分别得出反比例函数与一次函数的解析式;把D(n,3)代入求出的反比例函数解析式即可求出点D的坐标;
(2)先求出一次函数解析式,再求点A和点B的坐标,然后用勾股定理即可求出AB得长;
(2)观察函数图象,写出符合条件时自变量x的取值范围即可.
(1)∵(6,-1)在比例函数y=![]() 的函数图象上,
的函数图象上,
∴代入后得![]() ,解得m=-6,故反比例函数解析式为y=
,解得m=-6,故反比例函数解析式为y=![]() .
.
∵D(n,3),
∴3=![]() ,
,
∴n=-2,
∴D(-2,3).
(2)设一次函数解析式为y=kx+b,把C (6,-1),D(-2,3)代入,得
![]() ,
,
解之得
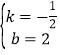 ,
,
∴![]() .
.
当x=0时,y=2;
当y=0时,x=4,
∴A(4,0),B(0,2),
∵AB=![]() ;
;
(3)根据函数图象可知,当x<-2或0<x<6时,一次函数的值大于反比例函数的值。
-
科目: 来源: 题型:
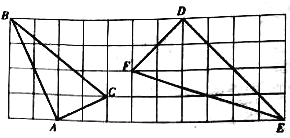
查看答案和解析>>【题目】如图,在由边长均为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点(网格线的交点)上,请按要求完成下列各题.
(1)试证明△ABC是直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知CB是⊙O的弦,CD是⊙O的直径,点A为CD延长线上一点,BC=AB,∠CAB=30°.
(1)求证:AB是⊙O的切线;(2)若⊙O的半径为2,求
 的长.
的长. 
-
科目: 来源: 题型:
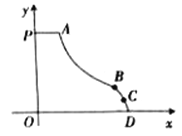
查看答案和解析>>【题目】如图所示的是一种新型的滑梯的示意图,其中线段PA是长为
 米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.
米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.(1)求滑道AB所在曲线的解析式;
(2)问小刚同学从点A滑到点C时,其下降的高度为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产了一款健身器材,可通过实体店和网上商店两种途径进行销售,销售了一段时间后,该企业对这种健身器材的销售情况进行了为期30天的跟踪调查,其中实体店的日销售量y1(套)与时间x(x为整数,单位:天)的部分对应值如下表所示:
时间x(天)
0
5
10
15
20
25
30
日销售量y(套)
0
25
40
45
40
25
0
(1)求出y1与x的二次函数关系式及自变量x的取值范围
(2)若网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的函数关系为
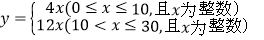 ,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值.
,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,若线段上的个点把这条线段分制为两部分,其中较长的一部分与全长之比等于
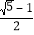 时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.(1)如图1,CD是△ABC的黄金分割线(AD> BD),△ABC的面积为4,求△ACD的面积 ;
(2)如图2,在△ABC中,∠A= 36°,AB=AC=1,过点B作BD平分∠ABC,与AC相交于点D,求证: BD是△ABC的黄金分割线.
(3)如图3,BE、CD是△ABC的黄金分割线(AD> BD,AE> CE),BE、CD相交于点O.
①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由;
②求
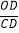 的值.
的值.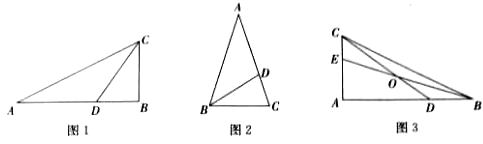
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-
 x+2
x+2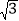 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )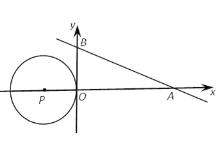
A. 3 B. 4 C. 5 D. 7
相关试题

