【题目】如图,已知CB是⊙O的弦,CD是⊙O的直径,点A为CD延长线上一点,BC=AB,∠CAB=30°.
(1)求证:AB是⊙O的切线;(2)若⊙O的半径为2,求![]() 的长.
的长.

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】解:(1)证明:如图,连接OB,
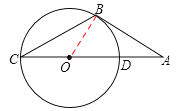
∵BC=AB,∠CAB=30°,∴∠ACB=∠CAB=30°。
又∵OC=OB,∴∠CBO=∠ACB=30°。
∴∠AOB=∠CBO+∠ACB=60°。
在△ABO中,∠CAB=30°,∠AOB=60°,∴∠ABO=90°,即AB⊥OB。
∴AB为圆O的切线。
(2)∵OB=2,∠BOD=60°,
∴![]() 的长度=
的长度=![]() 。
。
(1)连接OB,如图所示,由BC=AB,利用等边对等角得到一对角相等,由∠CAB的度数得出
∠ACB的度数,再由OC=OB,利用等边对等角得到一对角相等,确定出∠CBO,由外角的性质求出∠AOB的度数,在△AOB中,利用三角形的内角和定理求出∠ABO为90°,可得出AB为圆O的切线。
(2)直接应用弧长公式计算即可。
-
科目: 来源: 题型:
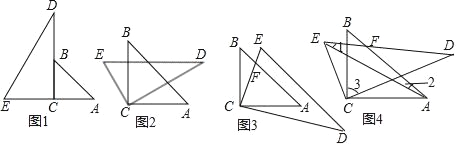
查看答案和解析>>【题目】将两块三角板按图1摆放,固定三角板ABC,将三角板CDE绕点C按顺时针方向旋转,其中∠A=45°,∠D=30°,设旋转角为α,(0°<a<80°)
(1)当DE∥AC时(如图2),求α的值;
(2)当DE∥AB时(如图3).AB与CE相交于点F,求α的值;
(3)当0°<α<90°时,连结AE(如图4),直线AB与DE相交于点F,试探究∠1+∠2+∠3的大小是否改变?若不改变,请求出此定值,若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:
 .唐诗;
.唐诗; .宋词;
.宋词; .论语;
.论语; .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
-
科目: 来源: 题型:
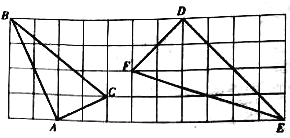
查看答案和解析>>【题目】如图,在由边长均为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点(网格线的交点)上,请按要求完成下列各题.
(1)试证明△ABC是直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由.
-
科目: 来源: 题型:
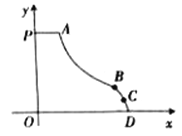
查看答案和解析>>【题目】如图所示的是一种新型的滑梯的示意图,其中线段PA是长为
 米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.
米的平台,滑道AB是反比例丽数图象的部分,滑道 BCD是二次函数y=-(x-5)2+2图象的部分,两滑道的连接点B为抛物线的顶点,且点C的横坐标为6.(1)求滑道AB所在曲线的解析式;
(2)问小刚同学从点A滑到点C时,其下降的高度为多少米?
-
科目: 来源: 题型:
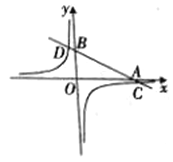
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y= kx +b(k≠0)的图象分别交x轴、y轴于A、B两点,与反比例函数y=
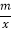 (m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).(1)求m的值和点D的坐标;
(2)求线段AB的长度;
(3)根据图象直接写出: 当x为何值时,一次函数的值大于反比例函数的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产了一款健身器材,可通过实体店和网上商店两种途径进行销售,销售了一段时间后,该企业对这种健身器材的销售情况进行了为期30天的跟踪调查,其中实体店的日销售量y1(套)与时间x(x为整数,单位:天)的部分对应值如下表所示:
时间x(天)
0
5
10
15
20
25
30
日销售量y(套)
0
25
40
45
40
25
0
(1)求出y1与x的二次函数关系式及自变量x的取值范围
(2)若网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的函数关系为
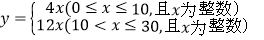 ,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值.
,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值.
相关试题

