【题目】如图,直线y=-![]() x+2
x+2![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
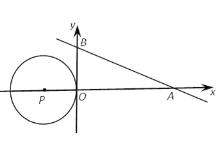
A. 3 B. 4 C. 5 D. 7
参考答案:
【答案】D
【解析】
根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
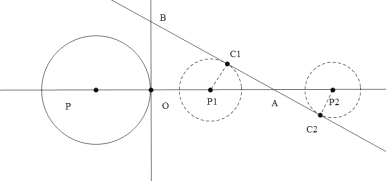
如图
∵直线y=-![]() x+2
x+2![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),
∴A点的坐标为0=-![]() x+2
x+2![]()
x=6, A(6,0),
B点的坐标为:(0,2![]() ),
),
∴AB=4![]()
将圆P沿x轴向左移动,当圆P与该直线相切于C1 时,P1C1 =2,
根据△AP1C1∽△ABO,![]() ∴AP 1 =4,
∴AP 1 =4,
∴P 1 的坐标为:(2,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2 时,P2C2 =2,
根据△AP2C2∽△ABO,![]() ∴AP2 =4,
∴AP2 =4,
P2 的坐标为:(10,0),
从2到10,当⊙P与该直线相交时,整数点有,3,4,5,6,7,8,9故横坐标为整数的点P的个数是7个
故选D
-
科目: 来源: 题型:
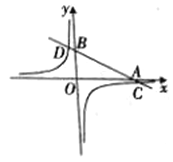
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y= kx +b(k≠0)的图象分别交x轴、y轴于A、B两点,与反比例函数y=
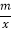 (m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).
(m≠0)的图象交于C、D两点。已知点C的坐标是(6,-1),D(n,3).(1)求m的值和点D的坐标;
(2)求线段AB的长度;
(3)根据图象直接写出: 当x为何值时,一次函数的值大于反比例函数的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产了一款健身器材,可通过实体店和网上商店两种途径进行销售,销售了一段时间后,该企业对这种健身器材的销售情况进行了为期30天的跟踪调查,其中实体店的日销售量y1(套)与时间x(x为整数,单位:天)的部分对应值如下表所示:
时间x(天)
0
5
10
15
20
25
30
日销售量y(套)
0
25
40
45
40
25
0
(1)求出y1与x的二次函数关系式及自变量x的取值范围
(2)若网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的函数关系为
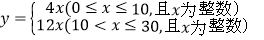 ,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值.
,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,若线段上的个点把这条线段分制为两部分,其中较长的一部分与全长之比等于
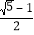 时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.(1)如图1,CD是△ABC的黄金分割线(AD> BD),△ABC的面积为4,求△ACD的面积 ;
(2)如图2,在△ABC中,∠A= 36°,AB=AC=1,过点B作BD平分∠ABC,与AC相交于点D,求证: BD是△ABC的黄金分割线.
(3)如图3,BE、CD是△ABC的黄金分割线(AD> BD,AE> CE),BE、CD相交于点O.
①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由;
②求
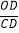 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠A=50°,∠E=45°,则∠F=____°.
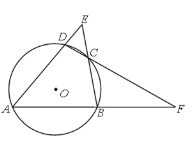
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有_______.(填序号)
x
…
-4
-3
-2
-1
0
1
…
y
…
-37
-21
-9
-1
3
3
…
①当x>1时,y随x的增大而减小. ②抛物线的对称轴为直线x=-
 .
.③当x=2时,y=-9. ④方程ax2+bx+c=0一个正数解
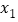 满足1<
满足1<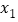 <2.
<2. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
相关试题

