【题目】如图,在△ABC中,AB=AC,∠BAC=90°,D,E分别在边BC,AC上,∠ADE=45°.
求证:△ABD∽△DCE.
参考答案:
【答案】证明:∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°.
∵∠ADC=∠ADE+∠EDC=45°+∠EDC,∠ADC=∠B+∠BAD=45°+∠BAD,
∴∠BAD=∠EDC,
∵∠B=∠C,∠BAD=∠EDC,
∴△ABD∽△DCE
【解析】根据等腰直角三角形的性质及三角形内角与外角的关系,易证△ABD∽△DCE.
【考点精析】本题主要考查了等腰直角三角形和相似三角形的判定的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点P为AC边上的动点,过点P作PD⊥AB于点D,则PB+PD的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区中学生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示尚不完整的统计图.

(1)请补全条形统计图;
(2)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 °;
(3)若该地区共有20000名中学生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,则BE与AF的数量关系是 .
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么上述结论还成立吗?请利用图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
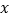 的二次方程
的二次方程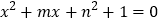 .
.(1)若
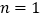 ,且此方程有一个根为
,且此方程有一个根为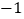 ,求
,求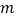 的值;
的值;(2)若
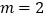 ,判断此方程根的情况.
,判断此方程根的情况.
相关试题

