Question

【题目】如图，Rt△ABC中，∠C=90°，AC=4，BC=3，点P为AC边上的动点，过点P作PD⊥AB于点D，则PB+PD的最小值为_____．

Answer 1

【答案】

【解析】

作点B关于AC的对称点B′，过点B′作B′D⊥AB于点D，交AC于点P，点P即为所求作的点，此时PB+PD有最小值，连接AB′，根据对称性的性质，BP=B′P，证明△ABC≌△AB′C，根据S△ABB′=S△ABC+S△AB′C=2S△ABC，即可求出PB+PD的最小值．

解：如图，作点B关于AC的对称点B′，过点B′作B′D⊥AB于点D，交AC于点P，点P即为所求作的点，此时PB+PD有最小值，连接AB′，根据对称性的性质，则BP=B′P，

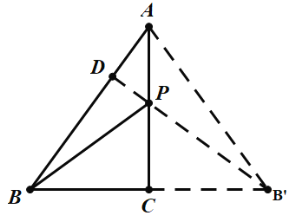
在Rt△ABC中，∠ACB=90°，AC=4，BC=3，

∴AB==5，

∵AC=AC，∠ACB=∠ACB′，BC=B′C，

∴△ABC≌△AB′C(SAS)，

∴S△ABB′=S△ABC+S△AB′C=2S△ABC，

即ABB′D=2×BCAC，

∴5B′D=24，

∴B′D=．

故答案为：．