【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(![]() ,
,![]() ).
).
[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.

参考答案:
【答案】M(2,1.5);(2)D(1,﹣1)或D(﹣3,5)或D(5,3).
【解析】试题分析:(1)先根据四边形ONEF是矩形,所以矩形的性质可以知道点M是对角线OE的中点,根据题中给出的线段的中点坐标公式即可得出M点的坐标;
(2)根据题意画出图形,然后分三种情况:①当AB为对角线时, ②当BC为对角线时, ③当AC为对角线时,求出点D的坐标.
解:(1)![]() 四边形ONEF是矩形,且
四边形ONEF是矩形,且![]() ,
,
![]() 点M是对角线OE的中点,
点M是对角线OE的中点,
![]() ,即
,即![]() .
.
因此,本题正确答案是:![]() ;
;
(2)如图所示:
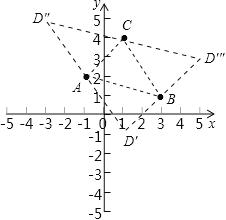
根据平行四边形的对角线互相平分可得:
设D点的坐标为![]() ,
,
![]() 以点A、B、C、D构成的四边形是平行四边形,
以点A、B、C、D构成的四边形是平行四边形,
①当AB为对角线时,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
②当BC为对角线时,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
D点坐标为![]() .
.
③当AC为对角线时,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
D点坐标为:![]() ,
,
综上所述,符合要求的点有:![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 的中垂线交
的中垂线交 于点
于点 交
交 延长线于点
延长线于点 .若
.若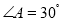 ,
,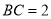 ,
, ,则四边形
,则四边形 的面积是( )
的面积是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

