【题目】如图1,某校有一块菱形空地ABCD,∠A=60°,AB=40m,现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH,其余部分种花草,园林公司修建鱼池,草坪的造价为y(元)与修建面积s(m2)之间的函数关系如图2所示,设AE为x米.

(1)填空:ED= m,EH= m,(用含x的代数式表示);
(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(2)若矩形鱼池EFGH的面积是300![]() m2,求EF的长度;
m2,求EF的长度;
(3)EF的长度为多少时,修建的鱼池和草坪的总造价最低,最低造价为多少元?
参考答案:
【答案】(1)![]() ;
;![]() ; (2)10m或30m;(3)x=20时,总造价最小,最小值为
; (2)10m或30m;(3)x=20时,总造价最小,最小值为![]() 元;
元;
【解析】
(1)直接写出结果即可.
(2)连接DB,判定△AEF为等边三角形,从而EF=x,利用(1)中EH的长,根据矩形面积公式列出方程,解出x即可.
(3)根据图2得出草坪和鱼池的价,分别求出草坪和鱼池的面积(用含x的式子表示),从而得到一个总价为一个关于x二次函数,将其写成顶点式,便可得出函数的最值.
(1)![]() ,
,![]() ;
;
(2)连接![]() ,则EF∥DB
,则EF∥DB
∴![]()
∵ ![]()
∴![]()
又![]()
∴△![]() 是等边三角形
是等边三角形
∴![]()
由(1)可知![]()
∴![]()
![]()
![]()
解得![]() ,
,![]() 经检验均符合题意,
经检验均符合题意,
答:![]() 的长度10
的长度10![]() 或30
或30![]() 。
。
(3)依题意得草坪单价为:4800÷80=60元/米2,
鱼池单价为:4800÷96=50元/米2,
∵四边形ABCD是菱形,∠BAD=60°,AB=40m,∴BD=40,AC=![]() ,
,
∴菱形ABCD的面积是:![]()
![]() ,
,
∵矩形EFGH的面积是:![]()
∴草坪的面积是:![]()
总造价为:![]()
![]()
![]()
∵![]()
∴当![]() 时,总造价最小,最小值为
时,总造价最小,最小值为![]() 元
元
答:EF的长度为20m时,修建的鱼池和草坪的总造价最低,最低造价![]() 元.
元.
故答案为:(1)![]() ;
;![]() ; (2)10m或30m;(3)x=20时,总造价最小,最小值为
; (2)10m或30m;(3)x=20时,总造价最小,最小值为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形纸片ABCD中,AB=3,BC=5.折叠纸片使点A落在边BC上的A′处,折痕为PQ.当点A′在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点A′在边BC上可移动的最大距离为( )

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)若原方程的一根大于3,另一根小于3,求k的最大整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABC的直角边的长是a,AD⊥BD,且AD=3BD,则△BCD的面积是_____.
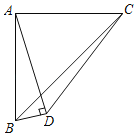
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个放置在地面上的长方体,长为15cm,宽为10cm,高为20cm,点B与点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
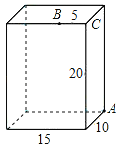
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,BE与CD交于点G.

(1)求证:AP=DG;
(2)求线段AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).
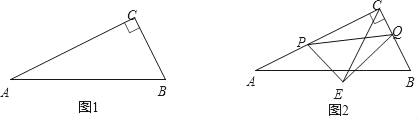
(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且
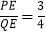 ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示).
相关试题

