【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①②
B.②③
C.①③
D.①②③
参考答案:
【答案】A
【解析】解:如图1,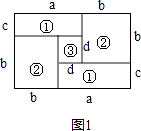 ,
,
设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,原来大长方形的周长是l,
则l=2(a+2b+c),
根据图示,可得![]()
·(1)﹣(2),可得:a﹣b=b﹣c,
∴2b=a+c,
∴l=2(a+2b+c)=2×2(a+c)=4(a+c),或l=2(a+2b+c)=2×4b=8b,
∴2(a+c)= ![]() ,4b=
,4b= ![]() ,
,
∵图形①的周长是2(a+c),图形②的周长是4b, ![]() 的值一定,
的值一定,
∴图形①②的周长是定值,不用测量就能知道,图形③的周长不用测量无法知道.
∴分割后不用测量就能知道周长的图形的标号为①②.
故选:A.
【考点精析】掌握中心对称及中心对称图形是解答本题的根本,需要知道如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
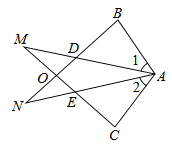
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
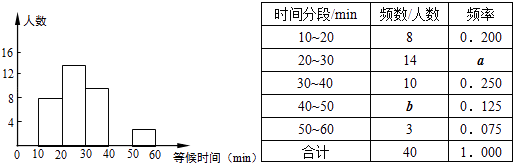
(1)这里采用的调查方式是(填“普查”或“抽样调查”),样本容量是;
(2)表中a= , b= , 并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:
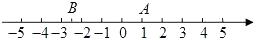
(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数.
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A,B的其它字母表示),并写出这些点表示的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明. 已知:如图,BE∥CD,∠A=∠1,

求证:∠C=∠E.
证明:∵BE∥CD (已知 )
∴∠2=∠C ()
又∵∠A=∠1 (已知 )
∴AC∥DE ()
∴∠2=∠E ()
∴∠C=∠E (等量代换 ) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题:
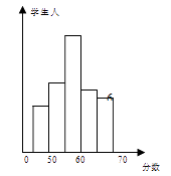
(1)该校参加语文知识竞赛学生共有多少人?
(2)成绩落在哪组数据范围内的人数最多?是多少?
(3)求成绩在80分以下的学生人数.
相关试题

