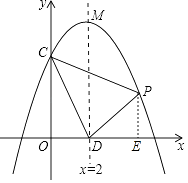
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
参考答案:
【答案】
(1)解:(1)∵OC=4,OD=2,
∴DM=6,
∴点M(2,6),
设y=a(x﹣2)2+6,代入(0,4)得:a=﹣ ![]() ,
,
∴该抛物线解析式为y=﹣ ![]() (x﹣2)2+6;
(x﹣2)2+6;
(2)(2)设点P(x,﹣ ![]() (x﹣2)2+6),即(x,﹣
(x﹣2)2+6),即(x,﹣ ![]() x2+2x+4),x>0,
x2+2x+4),x>0,
过点P作x轴的垂线,交x轴于点E,
则PE=﹣ ![]() x2+2x+4,DE=x﹣2,
x2+2x+4,DE=x﹣2,
S= ![]() x(﹣
x(﹣ ![]() x2+2x+4+4)﹣
x2+2x+4+4)﹣ ![]() ×2×4﹣
×2×4﹣ ![]() (x﹣2)(﹣
(x﹣2)(﹣ ![]() x2+2x+4),
x2+2x+4),
即S=﹣ ![]() x2+4x=﹣
x2+4x=﹣ ![]() (x﹣4)2+8,
(x﹣4)2+8,
∴当x=4时,S有最大值为8.
【解析】(1)由OC与OD的长,求出MD的长,确定出M坐标,设y=a(x﹣2)2+6,把C坐标代入求出a的值,即可确定出抛物线解析式;(2)由抛物线解析式设出P坐标,过点P做x轴的垂线,交x轴于点E,利用表示出的点P的坐标确定出线段PE、DE的长,用梯形OCPE的面积减去直角三角形OCD的面积和直角三角形PDE的面积,进而得出S与x的函数解析式,利用二次函数性质求出S最大值时x的值即可.
-
科目: 来源: 题型:
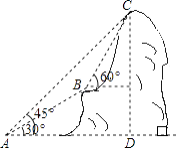
查看答案和解析>>【题目】如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
-
科目: 来源: 题型:
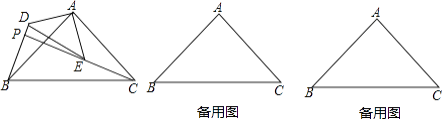
查看答案和解析>>【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值. -
科目: 来源: 题型:
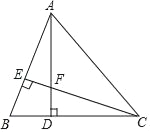
查看答案和解析>>【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填表:
a
0.000 001
0.001
1
1 000
1 000 000
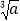
0.01
0.1
1
10
100
(2)由上表你发现了什么规律?请用语言叙述这个规律:被开方数扩大_____;
(3)根据你发现的规律填空:
①已知
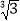 =1.442,则
=1.442,则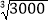 =______,
=______,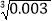 =______;
=______;②已知
 =0.076 97,则=______.
=0.076 97,则=______. -
科目: 来源: 题型:
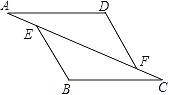
查看答案和解析>>【题目】如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.
(1)AD与BC相等吗?请说明理由;
(2)BE与DF平行吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
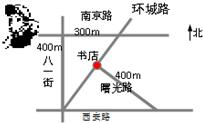
A、600mB、500m
C、400mD、300m
相关试题

